Derivatives are a central concept in calculus that describe how a function changes at any given point. Essentially, they measure the rate of change or the slope of a function’s graph, making them essential for understanding motion, growth, and many real-world applications in science, engineering, and economics.
This worksheet provides a variety of exercises to help you practice finding derivatives of different types of functions, including polynomials, exponential functions, and trigonometric functions. By working through these problems, you will reinforce your understanding of key differentiation rules and gain confidence in applying them to solve problems.
Differentiate the following functions:
1) 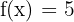
2) 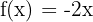
3) 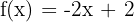
4)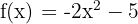
5) 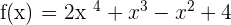
6) 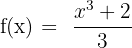
7) 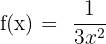
1) 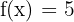
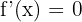
2) 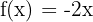

3) 

4) 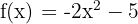
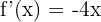
5) 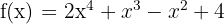
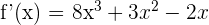
6) 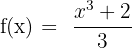
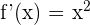
7) 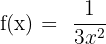
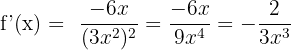
Differentiate the following functions using the power rule:
1) 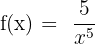
2) 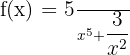
3) 
4) 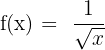
5) 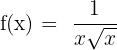
6) 
7) 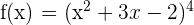
Differentiate the following functions using the power rule:
1) 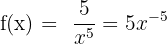
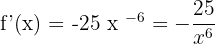
2) 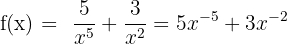
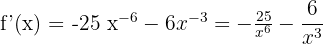
3) 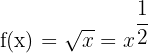
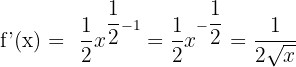
4) 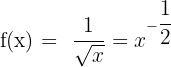
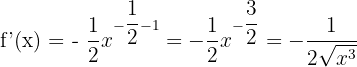
5) 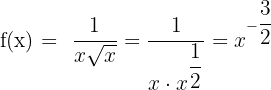
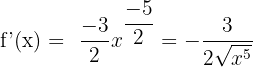
6) 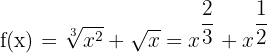
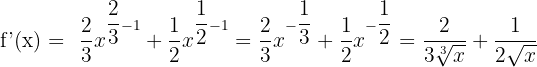
7) 
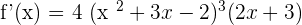
Differentiate the following functions:
1) 
2) 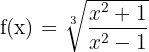
Differentiate the following functions:
1) 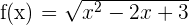
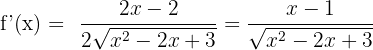
2) 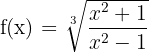
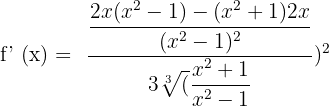
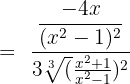
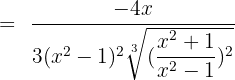
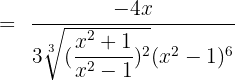
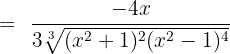
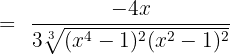
Differentiate the following exponential functions:
1) 
2) 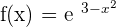
3) 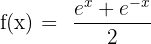
4) 
5) 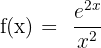
Differentiate the following exponential functions:
1) 
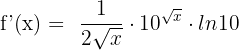
2) 
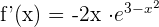
3) 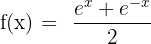
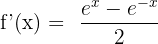
4) 
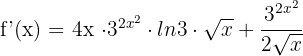
5) 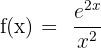
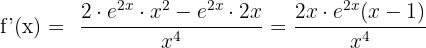
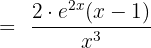
Differentiate the following logarithmic functions:
1) 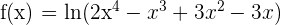
2) 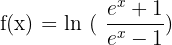
3) 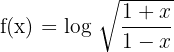
4) 
5) 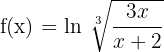
6) 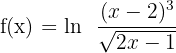
Differentiate the following logarithmic functions:
1) 
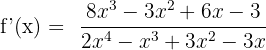
2) 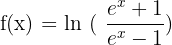
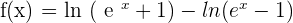
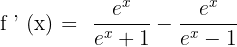
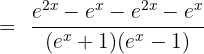
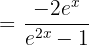
3) 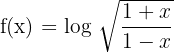
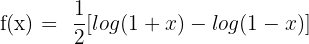
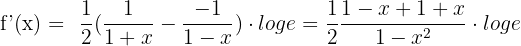

4) 
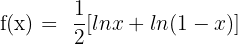
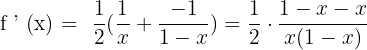
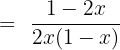
5) 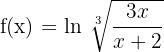
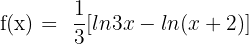
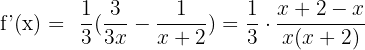
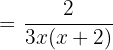
6) 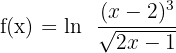
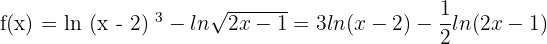
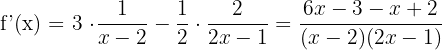
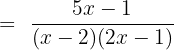
Summarise with AI:



Like the explanation, want to rearn more. Really enjoying the documents received.