Chapters
- Derivative Rules
- Derivative of a Constant
- Derivative of Constant Multiple
- Derivative of x
- Power Rule
- Derivative of a Root
- Derivative of a Sum or Difference
- Product Rule
- Quotient Rule
- Reciprocal Rule
- Derivative of an Exponential Function
- Derivative of a Logarithmic Function
- Derivative of a Sine Function
- Derivative of a Cosine Function
- Derivative of a Tangent Function
- Derivative of a Cotangent Function
- Derivative of a Secant Function
- Derivative of a Cosecant Function
- Derivative of an Arcsine
- Derivative of an Arccosine
- Derivative of an Arctangent
- Derivative of an Arccotangent
- Derivative of an Arcsecant
- Derivative of an Arccosecant
- Chain Rule
- Derivative of an Implicit Function
In this article, we will discuss rules of derivatives which are helpful to differentiate complex functions. But before proceeding to discuss the derivative rules, let us first see what are derivatives.
"A derivative of a function is an instantaneous rate of change of the function at a specific point"
In other words, we can say that the derivatives of the functions depict the rate of change of a particular function at a given point. Differentiation refers to the process of finding the derivatives of a function. We use derivatives to solve problems in calculus and differential equations. In geometry, the derivative of a function can be referred to as a slope of the function. If you remember, we define slope as:
"Rate of change of the dependent variable "y" with respect to the independent variable "x".
If f(x) is a function, then we can denote the derivative of function like this:
 =
= 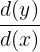 =
= 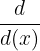
In the next section, we will discuss various rules of derivatives.

Derivative Rules
Derivative rules are also termed as differentiation rules. We have compiled all the derivative rules in this article below.
Derivative of a Constant
The derivative of a constant is equal to zero. Suppose, 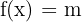 is a function, where m is a constant. Its derivative will be written as:
is a function, where m is a constant. Its derivative will be written as:
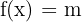
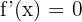
Derivative of Constant Multiple
If in a function, a constant is multiplied by the variable, then the derivative of such as function will be the constant multiplied by the derivative of the variable. Suppose 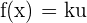 is a function in which k is a constant and u is a variable. The derivative of such a function will be written like this:
is a function in which k is a constant and u is a variable. The derivative of such a function will be written like this:
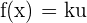

Derivative of x
The derivative of the variable x is equal to 1. Mathematically, we can denote it as:


Power Rule
We find the derivative of the function having an exponent or power like this:

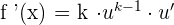
Derivative of a Root
We can be asked to differentiate the root functions. The derivative of a square root function is calculated like this:
If  is a function, then its derivative will be written as:
is a function, then its derivative will be written as:
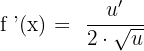
We can have the root functions that are not square roots. Instead, they can be cube root and quad root, etc. types of functions. In such cases, the derivatives of the functions will be computed like this:
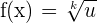
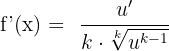
Derivative of a Sum or Difference
The derivatives of the functions that involve the arithmetic operations of addition and subtraction are calculated like this:

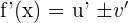
Product Rule
The derivative of the function that involves a multiplication operation is calculated like this:
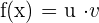

Quotient Rule
The derivatives of two differentiable functions which have a division sign between them is computed in this way:
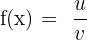
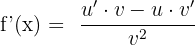
If the numerator has a constant, then we will compute the derivative like this:
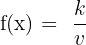
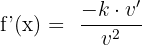
Reciprocal Rule
The reciprocal is inverse of a function. For instance, the reciprocal of the function 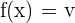 will be
will be 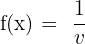 . We use the following rule to differentiate a reciprocal:
. We use the following rule to differentiate a reciprocal:
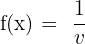
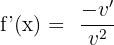
Derivative of an Exponential Function
In mathematics, the exponential functions are given in this form:

Here, y is the dependent variable, a is the base and x is an independent variable. In other words, we can say that the exponential functions have independent variable as their powers or exponents. The derivative of the exponential function is calculated by multiplying the derivative of the exponent, the function itself and logarithm of the base of the function.
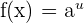

The derivative of the function in which the base is the natural number is calculated like this:

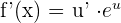
Derivative of a Logarithmic Function
The inverse of an exponential function is referred to as a logarithmic function. The derivative of a logarithmic function having a base is computed like this:
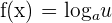
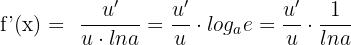
A logarithmic function, with base 10 is known as a common logarithm. Decadic logarithm is another name given to this type of a function. When we encounter a logarithmic function, in which no base is mentioned, then we automatically assume that the base of the function is 10. The derivative of such as function will be computed like this:
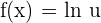
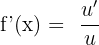
Derivative of a Sine Function
The derivative of a sine function is equal to the derivative of the function multiplied with cosine of the same function. For example, if we have a function 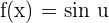 , then its derivative will be calculated in this way:
, then its derivative will be calculated in this way:
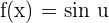
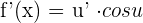
Derivative of a Cosine Function
The derivative of a cosine function is equal to the derivative of the function with a negative sign multiplied by sin of the same function.

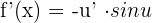
Derivative of a Tangent Function
The derivative of a tangent function will be computed like this:
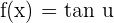

Derivative of a Cotangent Function
The derivative of the cotangent function is computed like this:
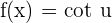
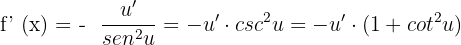
Derivative of a Secant Function
We differentiate a secant function f(x) = sec u like this:
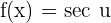
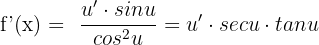
Derivative of a Cosecant Function
The cosecant function is differentiated like this:
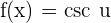
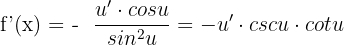
Derivative of an Arcsine
If we are given an arcsine function f(x) = arcsin u, then we calculate its derivative like this:
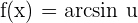
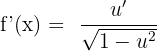
Derivative of an Arccosine
If we have to differentiate an arccosine function f(x) = arccos u, then we use the following rule:

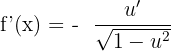
Derivative of an Arctangent
An arctangent function f(x) = arctan u is differentiated like this:
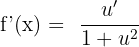
Derivative of an Arccotangent
The derivative of a function f(x) = arc cot u is calculated in this way:
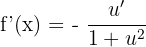
Derivative of an Arcsecant
The derivative of the function f(x) = arc sec u is calculated like this:
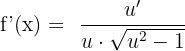
Derivative of an Arccosecant
The derivative of the function f(x) = arccsc u is calculated in this way:
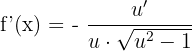
Chain Rule
To find the derivative of a composite function, we employ the derivative chain rule. A composite function reflects a situation in which we are given a function within another function or we have a function of a function. For example, if the function f and g are differentiable, then their composite is written as f o g or f(g(x)). The derivative of the composite function is calculated in this way:
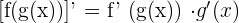
Derivative of an Implicit Function
The implicit function is written in terms of both the independent and dependent variables. The derivative of an implicit function y is calculated like this:
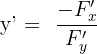
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.