Chapters
In this article, we will discuss how to compute the logarithmic derivative with examples. Before discussing how to compute the derivative of a logarithmic function, first, let us recall the definition of a derivative.
An instantaneous rate of change of a function at a given point is known as derivative
The procedure of finding the derivative of the function is known as differentiation. Mathematically, the derivative of the function f(x) is denoted as follows:
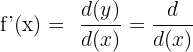
Geometrically, the derivative of the function is represented as slope because slope tells us the rate of change of the function at a point. Integration is inverse process of the differentiation.

Exponential vs Logarithmic Functions
You will be familiar with the exponential functions. The exponential functions are of the form:

Here, a = base of the function
y = Dependent variable
x = Independent variable as an exponent
You can see that in an exponential function, the exponent of the base is an independent variable. In other words, the attribute that uniquely describes the exponential functions is that their powers or exponents are the independent variables.
A logarithmic function is an inverse of the exponential function. For instance, the exponential function  is written like this in logarithmic form:
is written like this in logarithmic form:
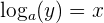
To convert the exponential function  into logarithmic form, we first identified the base " a" of the function. This base "a" of the exponential equation was written as base of the converted logarithmic function. The other two variables y and x changed their positions, i.e. x was moved to the right hand side of the equation and y to the left hand side of the equation. Before the base, we wrote log, and hence in this way we converted the exponential form of the equation to a logarithmic form.
into logarithmic form, we first identified the base " a" of the function. This base "a" of the exponential equation was written as base of the converted logarithmic function. The other two variables y and x changed their positions, i.e. x was moved to the right hand side of the equation and y to the left hand side of the equation. Before the base, we wrote log, and hence in this way we converted the exponential form of the equation to a logarithmic form.
A common logarithmic function has a base of 10 and a natural logarithm has a base e. The value of the base e in natural logarithms is equal to 2.71828.. If we are given a logarithmic function, in which no base is given, then we assume that the base of that function is equal to 10.
Derivative Rule of a Logarithmic Function
We employ the following derivative rule to differentiate a logarithmic function:
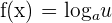
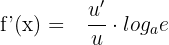
Because the 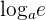 can be written as
can be written as 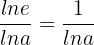 , hence we can also express the derivative of the logarithmic function like this:
, hence we can also express the derivative of the logarithmic function like this:
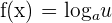
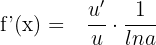
In the next section of the article, we will solve some examples in which we will differentiate the logarithmic function using the logarithmic rule of the derivative.
Example 1
Differentiate the following logarithmic function:
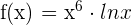
Solution
Since there are two functions separated by the multiplication sign, therefore, we will use the derivate product rule first.
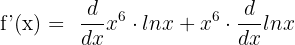
We will use the derivative power rule to differentiate 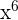 and logarithmic derivative rule to differentiate
and logarithmic derivative rule to differentiate  .
.
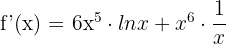
= 
Example 2
Differentiate the following function:
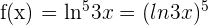
Solution
We will use the derivative power rule to differentiate the above function before using the derivative logarithmic rule:
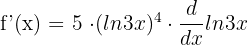
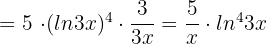
Example 3
Differentiate 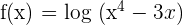
Solution
Use the derivative logarithmic rule 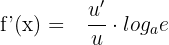 here:
here:
In this example,  .
.
We will differentiate each element separately in the numerator by applying the derivative product rule and derivative rule when constant is multiplied with a variable:
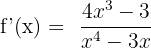
Example 4
Differentiate 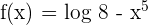 .
.
Solution
We will differentiate log 8 and  separately like this:
separately like this:
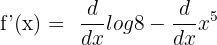
The derivative of log 8x is equal to 0 and the derivative of  is equal to
is equal to 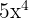 :
:
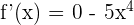
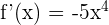
Example 5
Differentiate 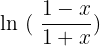 .
.
Solution
We can write the above function as:
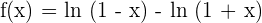
Apply logarithmic derivative rule here:
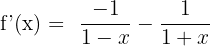
Now, we will solve the above expression as we solve the fractions which have addition or subtraction sign between them:
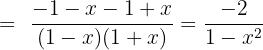
Example 6
Differentiate 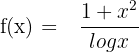 .
.
Solution
First, we will use the derivative quotient rule because we have two functions in the numerator and the denominator. According to the derivative quotient rule if 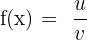 , then
, then 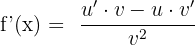 . The derivative of the function
. The derivative of the function  is equal to 2x and the derivative of the function log x is equal to
is equal to 2x and the derivative of the function log x is equal to  .
.
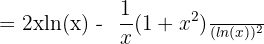
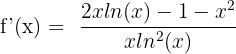
Example 7
Differentiate 
Solution
We will use the derivative product rule here because two functions are multiplied together:
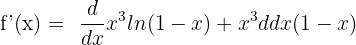
The derivative of the function  is equal to
is equal to 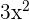 according to the derivative power rule, and the derivative of the function ln(1 - x) is equal to
according to the derivative power rule, and the derivative of the function ln(1 - x) is equal to 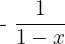 :
:
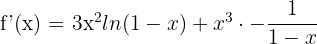
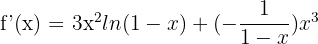
Simplify the above expression like this:
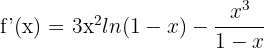
Example 8
Differentiate 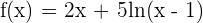
Solution
Since the above function has a positive sign between different elements of it that themselves are differentiable, hence we will use the derivative sum rule here. To use the derivative sum rule, we need to differentiate each element separately:
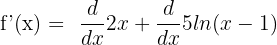
The derivative of the function 2x is equal to 2 and the derivative of the function 5ln(x - 1) is equal to 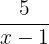 .
.
Example 9
Differentiate 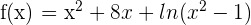 .
.
Solution
We will use the derivative sum or difference rule here first before using the logarithmic rule afterwards. According to the sum-difference rule of the differentiation, if  , then
, then 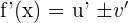 :
:
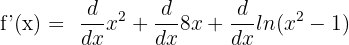
The derivative of the function  is equal to 2x, 8x is equal to 8 and
is equal to 2x, 8x is equal to 8 and  is equal to
is equal to 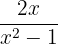
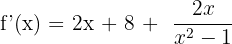
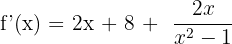
We can write the final answer by combining the functions 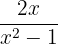 and
and  like this:
like this:
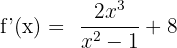
Example 10
Differentiate 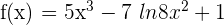
Solution
We will use the derivative sum or difference rule here because we have two functions segregated by the negative sign. According to the derivative sum/difference rule if if  , then
, then 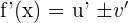 :
:
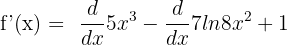
The derivative of the function 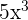 is equal to
is equal to 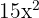 .
.
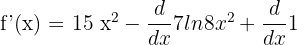
The derivative of the function 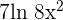 is equal to
is equal to 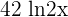 :
:
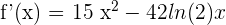












Like the explanation, want to rearn more. Really enjoying the documents received.