Chapters
The derivative of a function is one of the fundamental mathematical concepts. The process by which we find the derivative of a given function is known as differentiation. You may have heard about integration, which is the inverse of differentiation. Finding a derivative of the function means to calculate the rate of change of the function at any given point. We calculate the rate of change by dividing the change in the independent variable represented as 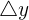 by the change in the dependent variable
by the change in the dependent variable 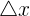 .
.

The derivative function is represented by 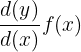 and is also known as instantaneous rate of change. The instantaneous rate of change is the rate of change in a function at a specific point.
and is also known as instantaneous rate of change. The instantaneous rate of change is the rate of change in a function at a specific point.

What are Exponential Functions
In this article, we will learn how to find the derivative of exponential functions. But before proceeding to how to find the derivative, let us recall what exponential functions are. A function in which the independent variable  is an exponent is known as an exponential function. The general notation of exponential function is given below:
is an exponent is known as an exponential function. The general notation of exponential function is given below:
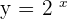
Here, y is the dependent variable, x is an independent variable and 2 is the base of the function.
Before finding the derivative of exponential functions, you should know how to find the derivative of the linear functions. It is because finding the derivative of exponential function also involves finding the derivative of its exponent which is often in the linear form. The slope intercept form of the linear functions is:

Here, m is the slope of a line, x is the independent variable and b is the constant. The derivative of a linear equation is equal to its slope  and the derivative of a constant function is 0.
and the derivative of a constant function is 0.
Method of Finding Derivative of Exponential Function
To find the derivative of an exponential function, follow these rules step by step:
Step 1
First, write the exponential function as it is. For example, if we need to find the derivative of the exponential function  , then we need to write this function as it is.
, then we need to write this function as it is.
Step 2
Calculate the logarithm of the base of the exponential function. For example, in the exponential function  , the base is e. Hence, the log of the base will be written as
, the base is e. Hence, the log of the base will be written as 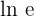
Step 3
Calculate the derivative of the exponent. In the exponential function, 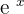 , the exponent is
, the exponent is  . The derivative of
. The derivative of  will be 1 because it is of the form
will be 1 because it is of the form  . Since, the value of m is 1, hence the derivative of
. Since, the value of m is 1, hence the derivative of  is 1.
is 1.
Step 4
Multiply the expressions obtained in step 1, step 2 and step 3 together to get the derivative of an exponential function. In the example, 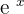 , the derivative will be:
, the derivative will be:
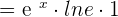
Here, e is a natural number whose value is equal to 2.71828.. The natural logarithms are represented as ln (e) and their values are equal to 1. Hence, the derivative of  .
.
Derivatives of Common Functions
We will go through some of the examples in this article which will clarify the concept of derivatives of exponential functions further. Before proceeding to examples, let us look at the following table which describes the derivatives of some common functions.
| Names of functions | Notation | Derivatives |
| Constant | b | 0 |
| Linear function | mx + b | m |
| Power | ||
| Trigonometry (i) | sin (x) | cos (x) |
| Trigonometry (ii) | cos (x) | - sin (x) |
| Trigonometry (iii) | tan (x) | |
| Square root | 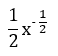 | |
| Logarithms | ln(x) | |
| Logarithms | 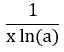 |
Derivatives Rules
Derivative rules are also known as differentiation rules. The following table shows some of the rules of derivatives:
| Rules | Functions | Derivatives |
|---|---|---|
| Multiplied by constant | af | |
| Power rule | ||
| Sum rule | a + b | |
| Difference rule | a - b | |
| Product rule | ab | |
| Quotient rule | a/b | 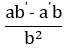 |
| Reciprocal rule | 1/a |
You can see that the derivative of a function whose power is 3 is a quadratic function.
Example 1
Find the derivative of the following function:

Solution
Follow the following step by step solution to find the derivative of the above function:
Step 1 - To find the derivative, first write the function  as it is.
as it is.
Step 2 - Now, find the derivative of the function in the power. The function in the power is a linear function  . Since, the derivative of a linear function is equal to its slope, hence the derivative of
. Since, the derivative of a linear function is equal to its slope, hence the derivative of  will be 2.
will be 2.
Step 3 - Take the log of the base. In the above example, the base is e which is a natural number. The natural log denoted by ln (e) is equal to 1.
Step 4 - Multiply the expressions obtained in step 1, 2 and 3 together to get the derivative of the exponential function:
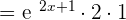

Example 2
Find the derivative of the following function:

Solution
Follow these steps to find how to differentiate the above function:
Step 1 - To find the derivative, first write the function  as it is.
as it is.
Step 2 - Find the log of the base. In the above exponential function, the base is 6, hence in the logarithmic form, it will be written as 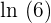 .
.
Step 3 - Find the derivative of the function in power. The power of the function is 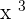 . We know that the derivative of the power function is denoted by
. We know that the derivative of the power function is denoted by 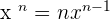 . Hence, using this rule we will get the derivative of the function
. Hence, using this rule we will get the derivative of the function  .
.
Step 4 - Multiply the expressions obtained in step 1, 2 and 3 together to get the derivative of the exponential function:
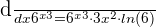
In the simplified form, we can write the answer as:
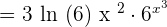
Example 3
Find the derivative of the following function:
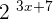
Solution
Step 1 - To find the derivative, first write the function 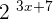 as it is.
as it is.
Step 2 - Now, find the derivative of the function in the power. The function in the power is a linear function 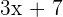 . Since, the derivative of a linear function is equal to its slope, hence the derivative of
. Since, the derivative of a linear function is equal to its slope, hence the derivative of 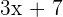 will be 3.
will be 3.
Step 3 - Take the log of the base. In the above example, the base is 2. The log of 2 will be written as  .
.
Step 4 - Multiply the expressions obtained in step 1, 2 and 3 together to get the derivative of the exponential function:
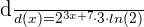
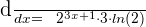
Example 4
Find the derivative of the following function:
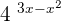
Solution
Follow these steps to find the derivative of the above function. We will use the rules of derivatives throughout this problem.
Step 1 - First, write the function as it is 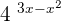 .
.
Step 2 - Next, we need to find the derivative of the function in power. The function in the power is 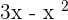 . According to the differential rule of derivative, we need to find the derivatives of both the functions separately. The derivative of the function
. According to the differential rule of derivative, we need to find the derivatives of both the functions separately. The derivative of the function  is 3 and the derivative of the function
is 3 and the derivative of the function 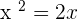 . Hence, we can write the expression in this step as
. Hence, we can write the expression in this step as 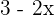 .
.
Step 3 - Find the log of the base. The log of 4 can be denoted as 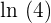 .
.
Step 4 - Multiply the expressions from step 1, 2 and 3 together to get the derivative of entire exponential function:
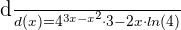
Example 5
Find the derivative of the following function:
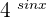
Solution
We will apply the differential trigonometry rule to solve this example.
Step 1 - First, write the function as it is 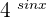 .
.
Step 2 - Now, find the derivative of the function in the exponent. The exponent of the function is a trigonometric function  . According to the derivative rules of trigonometric functions, the derivative of a sine function is equal to the cosine of the same function. Hence,
. According to the derivative rules of trigonometric functions, the derivative of a sine function is equal to the cosine of the same function. Hence,  .
.
Step 3 - In this step, we will find the log of the base. Since in the above exponential function, the base is 4, hence when we will take the log, we will write it as 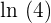 .
.
Step 4 - Multiply the expressions obtained in step 1, 2 and 3 together to get the derivative of the whole exponential function:
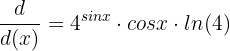
Example 6
Find the derivative of the following function:
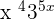
Solution
The above function is a product of two exponential functions. Therefore, we will use the derivative product function rule to find the derivative of the above function. According to the derivative product rule:
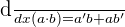
Step 1 - First find the derivative of 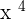 . We will use the derivative power rule to find the derivative of
. We will use the derivative power rule to find the derivative of 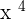 . According to the derivative power functions rule,
. According to the derivative power functions rule, 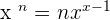 . Hence, the derivative of
. Hence, the derivative of 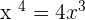 .
.
Step 2 - In this step, we need to find the derivative of 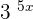 . The derivative of the exponent
. The derivative of the exponent  is equal to 5. The log of base 3 will be written as
is equal to 5. The log of base 3 will be written as 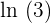 . The original function will be multiplied as it is because it is an exponential function. Hence, the derivative of the entire function is
. The original function will be multiplied as it is because it is an exponential function. Hence, the derivative of the entire function is 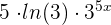 .
.
Step 3 - Use the product rule 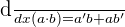 to write the derivative of the function like this:
to write the derivative of the function like this:

Example 7
Find the derivative of the following function:
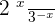
Solution
Since the above function is in the fractional form, hence we will apply the derivative quotient rule for differentiating this function. According to the derivative quotient rule:
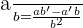
In the above example, 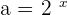 and
and  .
.
Step 1 - Find the derivative of the numerator. Since it is in the exponential form, hence we will differentiate it like this:
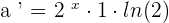
Step 2 - Find the derivative of the denominator b like this:

Step 3 - Use the derivative quotient rule 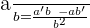 to write the derivative of the entire exponential function:
to write the derivative of the entire exponential function:
= 
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.