We all know what is a function. When we derivate a function at a specific point, we get the slope at that point. You can also call it the rate of change because a derivative is basically a rate of change of both components (here we are talking about x and y axes). In simple words, derivative of a function provides valuable information which can help a lot, especially in scientific researches.

How To Find Derivative of a Function
A function defines a relationship between the independent variable and the dependent variable. Let's pick an example of a displacement and time equation, 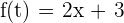 . The displacement is an independent variable, however, time is a dependent variable. Hence, we can say that time varies according to the distance and that is true in real life too. The longer your distance, the more time you require (assuming speed is constant) but what about distance? What thing varies distance? Nothing! That is why it is called independent but what if we derivate the time with respect to the distance? Let's find out!
. The displacement is an independent variable, however, time is a dependent variable. Hence, we can say that time varies according to the distance and that is true in real life too. The longer your distance, the more time you require (assuming speed is constant) but what about distance? What thing varies distance? Nothing! That is why it is called independent but what if we derivate the time with respect to the distance? Let's find out!
The derivative function of a function  is a function that associates to each real number its derivative, if it exists. It is denoted by
is a function that associates to each real number its derivative, if it exists. It is denoted by  .
.

Let's try to find the derivative of our time equation:
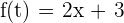

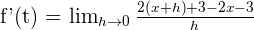

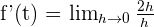

The answer  is the velocity of the distance-time equation. If you look closely, it is the change in displacement per unit time
is the velocity of the distance-time equation. If you look closely, it is the change in displacement per unit time 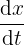 . This is the formula of velocity, now you see how you can calculate the velocity with the help of a distance time graph?
. This is the formula of velocity, now you see how you can calculate the velocity with the help of a distance time graph?
Examples
Calculate the derivative function of 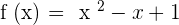 .
.


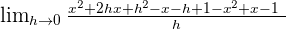
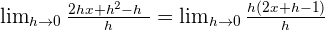
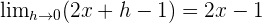
Find 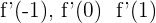 .
.
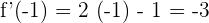
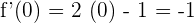

Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.