Chapters
One of the most difficult concepts of calculus is finding the derivative of an inverse function. In this article, we will see what is the inverse of a function, what is inverse function rule, and how to find a derivative of the inverse of the function. In addition to this, we will also apply the inverse function rules to trigonometric functions. So, let's get started with the introduction to inverse functions first.

What are the Inverse Functions?
An inverse function is also known as an "anti function". As the name implies, an inverse of the function reverses the original function. For example, if we put x in the original function and it gives the result y, then inputting y in the inverse or anti function will yield x. We can mathematically denote the relationship between the original function and its inverse like this:
If  , then
, then  or
or  , then
, then 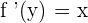
Here, f(x) is the original function and g(y) is its inverse or anti function. Inverse of a function is also denoted by  or
or 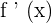 .
.
Flow Diagram of Inverse Function
Let us explain the concept further through the following flow diagrams. Consider a function  . The flow diagram of this function is drawn below.
. The flow diagram of this function is drawn below.

This flow diagram shows that when  is multiplied by 4, we get
is multiplied by 4, we get  . Finally, after subtracting 7 from
. Finally, after subtracting 7 from  , we get the original function
, we get the original function  .
.
Now, we will reverse all the arithmetic operations of the function  to get its inverse function. The flow diagram of the anti function of
to get its inverse function. The flow diagram of the anti function of  will look like this:
will look like this:

The above flow diagram shows that when 7 is added to  , we get
, we get 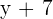 . After dividing by 4, we get the function
. After dividing by 4, we get the function 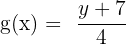 .
.
You can also compare and contrast the flow diagrams of the function and its inverse. If the original function goes through multiplication by 4, then while finding its inverse, the function is divided by 4. The same happens with the other arithmetic operations such as addition and subtraction. This shows that the arithmetic operations are reversed in the inverse function.
Example 1
If 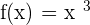 , then find f(x) and f ' (x) for the following input values.
, then find f(x) and f ' (x) for the following input values.
a) x = 3
b) x = 5
Solution
a) x = 3
Put x = 3 into the function 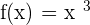 .
.

27 is the output of the original function. if we input the value of x = 3. Now, let us find the inverse of the function.
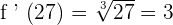
b) x = 5
Put x = 5 into the function 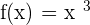 .
.
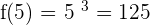
125 is the output of the original function, if we input the value of x = 3. Now, let us find the inverse of the function.
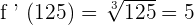
Inverse Function Rule
Inverse function rule says that if  , then
, then 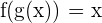 .
.
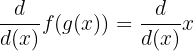

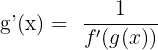
The inverse function rule is the fundamental theorem of calculus. You can use this theorem to find the derivatives of the inverses of functions.
Example 2
If  is the inverse function for
is the inverse function for 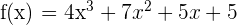 . Compute the value of
. Compute the value of 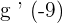 .
.
Solution
We will solve the question step by step using the derivative inverse rule.
Step 1
In this step, we will find the derivative of the original function  using the derivative sum and power rules which are important differentiation rules.
using the derivative sum and power rules which are important differentiation rules.
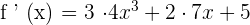
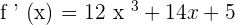
Step 2
In this step, we need to find out the value of  in such a way that
in such a way that  . In other words, we can say that
. In other words, we can say that 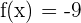 .
.
We will set the original function equal to -9.

Now by looking at the function we can see that if we plug  in the original function, we will get the answer -9.
in the original function, we will get the answer -9.
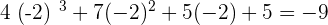
Step 3
Now, we will put together all the values in the inverse function rule to get the answer. The inverse function rule says that 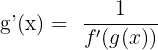 .
.
If  , then it means that
, then it means that 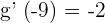 .
.
Plug the values in the main rule like this:
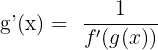
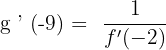
We know that 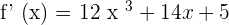
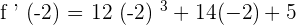
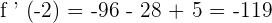
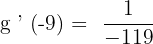
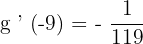
Example 3
If g(x) is the inverse function for  . Find the value of
. Find the value of 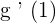 .
.
Solution
To calculate the value of 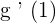 , we will follow the steps below.
, we will follow the steps below.
Step 1
We know that the original function  in this problem is a differentiable function. In this step, we will find the derivative of the original polynomial function
in this problem is a differentiable function. In this step, we will find the derivative of the original polynomial function  using one of the rules of differentiation known as the differentiation power rule. We already know that the process of finding the derivative of a function is known as differentiation. So, in other words, we will differentiate the algebraic expression.
using one of the rules of differentiation known as the differentiation power rule. We already know that the process of finding the derivative of a function is known as differentiation. So, in other words, we will differentiate the algebraic expression.


Step 2
In this step, we need to find out the value of  in such a way that
in such a way that  . In other words, we can say that
. In other words, we can say that 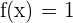 .
.
We will set the original function equal to 1.
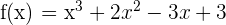
Now by looking at the function we can see that if we plug  in the original function, we will get the answer 1.
in the original function, we will get the answer 1.
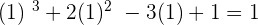
Step 3
Now, we will put together all the values in the inverse function rule to get the answer. The inverse function rule says that 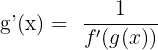 .
.
If  , then it means that
, then it means that  .
.
Plug the values in the main rule like this:
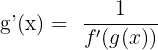
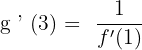
We know that  .
.
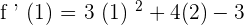
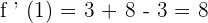
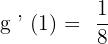
Trigonometric Functions
In trigonometry, there are six functions. These functions are known as trigonometric functions. Each trigonometric function has its inverse. We can use the inverse function rule to find the derivatives of these trigonometric functions.
Example 4
Differentiate using the derivative of the inverse function  .
.
Solution

If  , then we can say that
, then we can say that 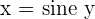 .
.
According to the derivative inverse rule 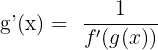 .
.
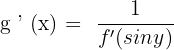
We know that the 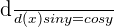 . Put this value in the formula:
. Put this value in the formula:
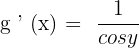
We know that 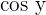 is equivalent to
is equivalent to 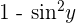
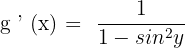
Remember that  , so we will rewrite it as:
, so we will rewrite it as:
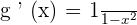
Derivatives of Inverse trigonometric Functions
You can easily find the derivatives of inverse trig functions using the inverse function rule, but memorizing them is the best idea. Hence, we have listed the derivatives of inverse trigonometric functions below so that you do not have to go through the complex procedure of differentiating the inverse of a trig function.
a) If  , then
, then 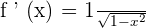
b) If  , then
, then 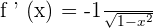
c) If  , then
, then 
d) If 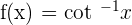 , then
, then 
e) If  , then
, then 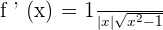
f) If 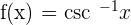 , then
, then 
Summarise with AI:












Like the explanation, want to rearn more. Really enjoying the documents received.