Chapters
In this article, we will discuss the derivative chain rule in detail. Before discussing the chain rule, first, we will recall the definition of derivatives.
The derivative of a function is defined as:
"An instantaneous rate of change of a function at a specific point"
The process of finding the derivatives of the functions is known as differentiation which is an important concept in differential calculus. The differentiation is quite helpful in solving the complex problems in calculus. The inverse of differentiation is known as integration. If we find the derivative of a function for the first time, then it is known as the first derivative. We can find the derivatives of the functions as many times as we can. It means finding the derivative of a derivative until it is not differentiable any further. When we find the derivatives of the same function multiple times, then the resulting derivatives are known as higher- order derivatives.
While doing the geometric interpretation of the derivatives, we identify the derivative of a function with the slope of its graph. This is because the slope of the graph tells us the rate of change of the dependent variable (y) with respect to the independent variable (x). We denote the derivative of a function like this:
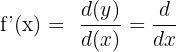

Rules of Derivatives
There are several rules of derivatives that make differentiation quite easy. The most prominent rules are the sum/differentiation rule, product rule, quotient rule, exponent rule, power rule, and chain rule. We also have derivative formulas for logarithmic functions, trigonometric functions, and their inverses. In this article, we will only focus on the derivative chain rule.
Derivative Chain Rule
We use the derivative chain rule when we have to compute the derivative of a composite function. The composite function is a function within a function or a situation in which we are given a function of a function. For instance, suppose the functions f and g are differentiable. Their composite will be written as f o g or f(g(x)). The derivative of the composite function is calculated by using the derivative chain rule given below:
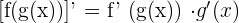
In the next section, we will solve some of the examples in which we will differentiate the composite functions using the derivative chain rule.
Example 1
Differentiate 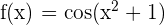 .
.
Solution
The above function is a composite function because it is written in the form f(g(x)). Here, we can say that 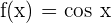 and
and  . Now, we will differentiate this function using the chain rule below;
. Now, we will differentiate this function using the chain rule below;
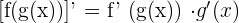
First, we will compute  . Recall that the derivative of cos x is equal to -sin x. Hence,
. Recall that the derivative of cos x is equal to -sin x. Hence, 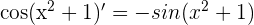 .
.
Now, calculate  . In this example,
. In this example,  . We will find its derivative by employing the derivative sum/difference and power rule. The derivative of
. We will find its derivative by employing the derivative sum/difference and power rule. The derivative of  is equal to 2x and the derivative of 1 is equal to 0. Hence,
is equal to 2x and the derivative of 1 is equal to 0. Hence,  . Substitute the values of
. Substitute the values of  and
and  in the below formula to get the derivative of the function in this example:
in the below formula to get the derivative of the function in this example:
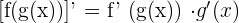
= 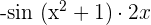
Example 2
Differentiate  .
.
Solution
First, we should immediately identify the above function as a composite function because it is written in the form of f(g(x)). Here, in this example, 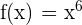 and
and 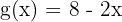 .
.
Let us first find  . If
. If 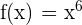 , then we can find its derivative using the power rule.
, then we can find its derivative using the power rule.
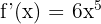
Now, we will compute the derivative of  . In this example, the inner function, i.e.,
. In this example, the inner function, i.e., 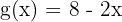 . Hence,
. Hence, 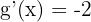 .
.
Substitute these values in the following formula:
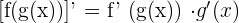
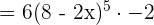
By simplifying the above expression, we will get the following answer:

Example 3
Find the derivative of the function  .
.
Solution
Again, the function in this example is a composite function because it is written in the form 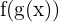 . Here,
. Here, 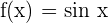 and
and 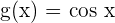 . First we will find the derivative of f(x) and then g(x).
. First we will find the derivative of f(x) and then g(x).
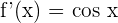

Substitute these values in the below formula to get the derivative:
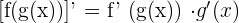
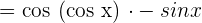
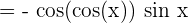
Example 4
Differentiate the function 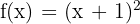 .
.
Solution
The above function is a composite function because it is written as 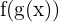 . Here,
. Here, 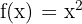 and
and 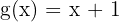 .
.
The derivative of the function  will be calculated using the derivative power rule and the derivative of the function
will be calculated using the derivative power rule and the derivative of the function  will be computed using the sum/difference rule.
will be computed using the sum/difference rule.

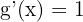
Substitute these values in the following formula of chain rule to get the derivative of the composite function in this example:
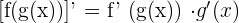
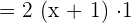
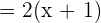
Example 5
Find the derivative of the function 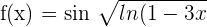 .
.
Solution
In this example, the function 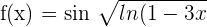 is a composite function because we have a function within a function. Here,
is a composite function because we have a function within a function. Here, 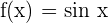 and
and  . The derivative of the function
. The derivative of the function  is easy to calculate as it is equal to cos x.
is easy to calculate as it is equal to cos x.
The other function, i.e.  is a logarithmic function, hence we will find its derivative using the formula below:
is a logarithmic function, hence we will find its derivative using the formula below:
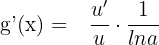
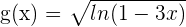
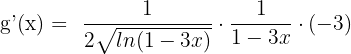
Substitute the values of  and
and  in the following formula to get the derivative:
in the following formula to get the derivative:
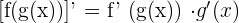
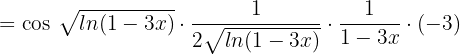
Example 6
Differentiate the function 
Solution
The above function is a composite function because it is written as 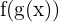 . Here,
. Here, 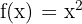 and
and  .
.
The derivative of the function  will be calculated using the derivative power rule and the derivative of the function
will be calculated using the derivative power rule and the derivative of the function  will be computed using the sum/difference rule.
will be computed using the sum/difference rule.

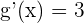
Substitute these values in the following formula of chain rule to get the derivative of the composite function in this example:
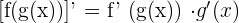
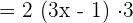
Simplify the above expression like this:
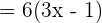
Example 7
Differentiate 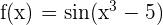 .
.
Solution
The above function is a composite function because it is written in the form f(g(x)). Here, we can say that 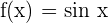 and
and 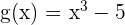 . Now, we will differentiate this function using the chain rule below;
. Now, we will differentiate this function using the chain rule below;
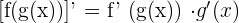
First, we will compute  . Recall that the derivative of sin x is equal to cos x.
. Recall that the derivative of sin x is equal to cos x.
Now, calculate  . In this example,
. In this example, 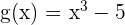 . We will find its derivative by employing the derivative sum/difference and power rule. The derivative of
. We will find its derivative by employing the derivative sum/difference and power rule. The derivative of  is equal to
is equal to 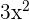 and the derivative of -5 is equal to 0. Hence,
and the derivative of -5 is equal to 0. Hence, 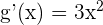 . Substitute the values of
. Substitute the values of  and
and 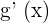 in the below formula to get the derivative of the function in this example:
in the below formula to get the derivative of the function in this example:
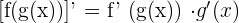
= 
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.