Chapters

Introduction to Derivatives
The process of finding a derivative is known as differentiation. The derivative of a function is defined as follows:
"A derivative of a function is an instantaneous rate of change of a function at a given point".
The derivative of a function is denoted as follows:
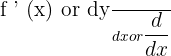
The derivative of a function  is
is 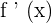 . The derivative
. The derivative 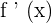 itself is a function that can be differentiated further. The derivative of a derivative of a function is known as as a second order derivative. We can continue to differentiate the derivatives of the functions further and name them as third, fourth, fifth... derivatives. These derivatives are known as higher order derivatives.
itself is a function that can be differentiated further. The derivative of a derivative of a function is known as as a second order derivative. We can continue to differentiate the derivatives of the functions further and name them as third, fourth, fifth... derivatives. These derivatives are known as higher order derivatives.
Types of Functions and Derivative rules
There are two types of functions, explicit and implicit functions. Explicit functions are the functions which are expressed as y = some function of the variable x. For example, 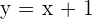 is an explicit function. Implicit functions are the functions in which the known value of x does not directly lead to the value of y. For example,
is an explicit function. Implicit functions are the functions in which the known value of x does not directly lead to the value of y. For example, 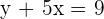 is an example of implicit function. The process of finding the derivative of an implicit function is known as implicit differentiation. You can differentiate the explicit functions using the following rules of differentiation.
is an example of implicit function. The process of finding the derivative of an implicit function is known as implicit differentiation. You can differentiate the explicit functions using the following rules of differentiation.
Constant rule 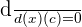
Power rule 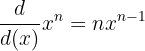
Sum rule 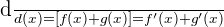
Difference rule 
Product rule 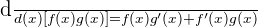
Quotient rule 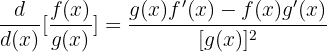
Chain-rule 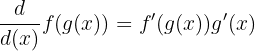
The above differentiation rules should be on your finger tips if you want to solve the calculus problems related to differentiation. Differentiation and integration are important concepts in calculus. The reverse or inverse of differentiation is known as integration. Differential calculus is a crucial sub-filed of calculus which deals with rates of change of the variable at a given point.
Do you know what one-sided derivative is? If not, we are here to explain this concept along with relevant examples.
What are One-Sided Derivatives?
When you differentiate or find a derivative of a function either from the left or from the right, then such derivative is known as a one-sided derivative.
Left Hand Derivative
The mathematical formula for finding the left hand derivative is given below:
 f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} \frac {f (a + h) - f(a)} {h}
f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} \frac {f (a + h) - f(a)} {h}
Right Hand Derivative
The right hand derivative is denoted mathematically as:
 f ' (a ^ {+}) = \lim_ {h \rightarrow 0 ^ {+}} \frac {f (a + h) - f(a)} {h}
f ' (a ^ {+}) = \lim_ {h \rightarrow 0 ^ {+}} \frac {f (a + h) - f(a)} {h}
A function is differentiable at a point if and only if it is differentiable from the left and right side and these derivatives coincide.
Theorem
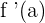 exists under these conditions:
exists under these conditions:
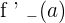 and
and 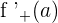 exist
exist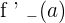 =
= 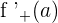
If the above two conditions are fulfilled, then the derivative  is equal to the same value of
is equal to the same value of 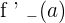 and
and 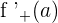 .
.
It should be kept in mind that if both left and right side derivatives are the same, then the derivative of the function is an ordinary derivative instead of one-sided derivative. See the following examples for further clarity of your concept related to one-sided derivatives.
Example 1
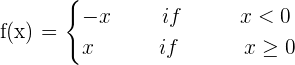
Solution
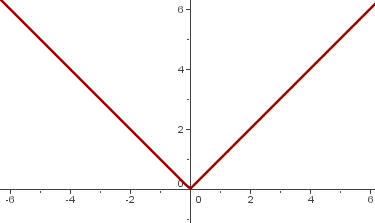
You can see that the above function is a piecewise function. With piecewise functions, it is necessary to study the derivatives at the points of lateral separation of the different pieces.
Follow these steps to determine if the function is differentiable at  or not.
or not.
Step 1 - Find the left hand derivative
The formula for finding the left hand derivative is:
 f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} \frac {f (a + h) - f(a)} {h}
f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} \frac {f (a + h) - f(a)} {h}
Since 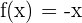 and
and 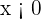 , hence we will put the values in the formula:
, hence we will put the values in the formula:
 \lim_{x \rightarrow 0 ^ {-}} \frac {-(0 + h) - 0} {h}
\lim_{x \rightarrow 0 ^ {-}} \frac {-(0 + h) - 0} {h}
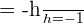
Step 2 - Find the derivative from the right
The formula for finding out the right hand derivative is given below:
 f ' (a ^ {+}) = \lim_ {h \rightarrow 0 ^ {+}} \frac {f (a + h) - f(a)} {h}
f ' (a ^ {+}) = \lim_ {h \rightarrow 0 ^ {+}} \frac {f (a + h) - f(a)} {h}
Since the second part of the function is  and
and 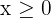 , hence we will put the values in the formula:
, hence we will put the values in the formula:
 \lim_{x \rightarrow 0 ^ {+}} \frac {0 + h - 0} {h}
\lim_{x \rightarrow 0 ^ {+}} \frac {0 + h - 0} {h}
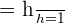
Step 3 - Compare the left and right hand derivatives
The left hand derivative is 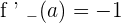 and the right hand derivative is
and the right hand derivative is 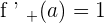 . Since
. Since 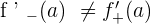 , therefore we can say that the function is not differentiable at
, therefore we can say that the function is not differentiable at  .
.
The graph of this piecewise function is given below.
Example 2
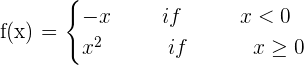
Solution
Step 1 - Find the left hand derivative
The formula for computation of the left hand derivative is:
 f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} \frac {f (a + h) - f(a)} {h}
f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} \frac {f (a + h) - f(a)} {h}
Since 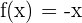 and
and 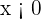 , hence we will put the values in the formula:
, hence we will put the values in the formula:
 \lim_{x \rightarrow 0 ^ {-}} \frac {-(0 + h) - 0} {h}
\lim_{x \rightarrow 0 ^ {-}} \frac {-(0 + h) - 0} {h}
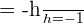
Step 2 - Find the right hand derivative
The formula for finding out the right hand derivative is given below:
 f ' (a ^ {+}) = \lim_ {h \rightarrow 0 ^ {+}} \frac {f (a + h) - f(a)} {h}
f ' (a ^ {+}) = \lim_ {h \rightarrow 0 ^ {+}} \frac {f (a + h) - f(a)} {h}
Since the second part of the function is 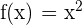 and
and 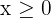 , hence we will put the values in the formula:
, hence we will put the values in the formula:
 \lim_{x \rightarrow 0 ^ {+}} \frac {(0 + h) ^ 2 - 0} {h}
\lim_{x \rightarrow 0 ^ {+}} \frac {(0 + h) ^ 2 - 0} {h}
 = \lim_{x \rightarrow 0 ^ {+}} \frac {h ^ 2} {h} = 1
= \lim_{x \rightarrow 0 ^ {+}} \frac {h ^ 2} {h} = 1
 = \lim_{x \rightarrow 0 ^ {+}} = 0
= \lim_{x \rightarrow 0 ^ {+}} = 0
Step 3 - Compare the left and right hand derivatives
The left hand derivative is 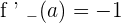 . Similarly, the right hand derivative is
. Similarly, the right hand derivative is 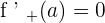 . Since
. Since 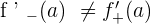 , therefore we can say that the function is not differentiable at
, therefore we can say that the function is not differentiable at  .
.
The function looks like this in the xy coordinate plane.
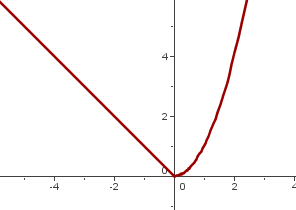
Example 3
Check whether the function 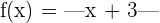 differentiable at
differentiable at 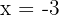 .
.
Solution
This function is an absolute-value function. We will follow the following steps to determine if the function 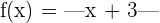 is differentiable at
is differentiable at 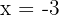 or not.
or not.
Step 1 - Find the left hand derivative
To compute the left hand derivative, we use the following formula:
 f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} \frac {f (a + h) - f(a)} {h}
f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} \frac {f (a + h) - f(a)} {h}
 f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} = \frac { |(-3 + h ) + 3 - f(-3)} {h}
f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} = \frac { |(-3 + h ) + 3 - f(-3)} {h}
 f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} = \frac {|(-3 + h) + 3| - 0} {h}
f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {-}} = \frac {|(-3 + h) + 3| - 0} {h}
 \lim_{h \rightarrow 0 ^ {-}} = \frac {|h|}{h}
\lim_{h \rightarrow 0 ^ {-}} = \frac {|h|}{h}
As this is a left hand derivative, so 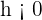
 \lim_{h \rightarrow 0 ^ {-}} = \frac {-h} {h} = -1
\lim_{h \rightarrow 0 ^ {-}} = \frac {-h} {h} = -1
Step 2 - Find the right hand derivative
The formula for finding out the right hand derivative is given below:
 f ' (a ^ {+}) = \lim_{h \rightarrow 0 ^ {+}} \frac {f (a + h) - f(a)} {h}
f ' (a ^ {+}) = \lim_{h \rightarrow 0 ^ {+}} \frac {f (a + h) - f(a)} {h}
 f ' (a ^ {+}) = \lim_{h \rightarrow 0 ^ {+}} = \frac { |(-3 + h ) + 3 - f(-3)} {h}
f ' (a ^ {+}) = \lim_{h \rightarrow 0 ^ {+}} = \frac { |(-3 + h ) + 3 - f(-3)} {h}
 f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {+}} = \frac {|h| } {h}
f ' (a ^ {-}) = \lim_{h \rightarrow 0 ^ {+}} = \frac {|h| } {h}
 \lim_{h \rightarrow 0 ^ {-}} = \frac {|h|}{h}
\lim_{h \rightarrow 0 ^ {-}} = \frac {|h|}{h}
As this is a right hand derivative, so 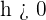
 \lim_{h \rightarrow 0 ^ {+}} = \frac {h} {h} = 1
\lim_{h \rightarrow 0 ^ {+}} = \frac {h} {h} = 1
Step 3 - Compare the left and right hand derivatives
The left hand derivative is 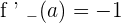 and the right hand derivative is
and the right hand derivative is 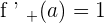 . Since
. Since 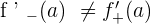 , therefore we can say that the function is not differentiable at
, therefore we can say that the function is not differentiable at  .
.













Like the explanation, want to rearn more. Really enjoying the documents received.