Chapters

Difference between Explicit and Implicit Functions
In mathematics, a function represents the relationship between two sets of values in such a way that each input value generates a single output value. There are two types of functions:
- Explicit function: When x is known, we can compute the value of y. It is expressed as y equal to some function of the variable x.
- Implicit function: Even when the value of x is known, we cannot directly compute the value of y.
Examples
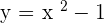 is an example of explicit function because knowing the value of x directly yields the value of y.
is an example of explicit function because knowing the value of x directly yields the value of y. is an example of implicit function because knowing the value of x does not directly lead us to the value of y. It is also not expressed as y equal to some function of x.
is an example of implicit function because knowing the value of x does not directly lead us to the value of y. It is also not expressed as y equal to some function of x.
Now that you know the difference between explicit and implicit functions, you can easily label whether the given function is in explicit or implicit form.
Differentiating Implicit Functions
We know that finding the derivative of a function is one of the fundamental concepts of calculus. The derivative of a function is defined as the instantaneous rate of change of the function at some point. The process of finding the derivative of a function is known as differentiation. We can compute multiple derivatives of the same function. When we differentiate the function first, the resultant derivative is known as the first derivative. When we differentiate the first derivative further, the resultant expression is known as second-derivative. In this article, we will only see how to find the first derivative of the implicit functions.
You should be familiar with the rules of differentiation before trying to find derivatives of functions. Some of the basic differentiation rules are given below.
- Constant rule :
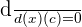
- Power rule :
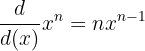
- Sum rule :
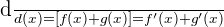
- Difference rule :

- Product rule :
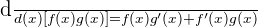
- Quotient rule (used for fractions):
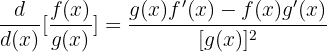
- Chain-rule :
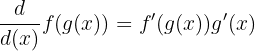
How to do Implicit Differentiation?
You may have probably done explicit differentiation multiple times because it is the basic kind of differentiation which involves applying the derivative rules. Have you ever wondered how to differentiate an implicit function and how this kind of differentiation is different from the explicit one? Well in this section we will learn how do we find a derivative of an implicit function from examples. But before proceeding to examples, let us first see the steps involved in the implicit differentiation of a function.
- Step 1: The first step of the implicit differentiation is to differentiate both sides of the function with respect to the variable
 . One thing to keep in mind is to multiply the derivative of the term involving the variable
. One thing to keep in mind is to multiply the derivative of the term involving the variable  with
with 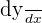 .
. - Step 2: In this step, we solve the equation for
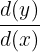 by isolating
by isolating 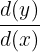 .
.
In other words, we can say that when we are given an implicit function, we use a chain rule to differentiate the function. The following examples will clarify this concept further.
Example 1
Differentiate 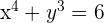
Solution
For your ease, we have broken down the solution of this problem into multiple steps.
Step 1 - Differentiate both sides of the function with respect to the variable x
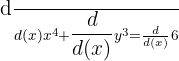
We will apply the derivative power rule to the left side and derivative constant rule to the right side of the function.
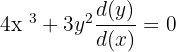
Since there was only a constant on right hand side of the equation, hence we have set the whole equation equal to 0. Besides differentiating each element in the function, the derivative of y is also multiplied by 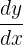 .
.
Step 2: Simplify the equation by solving for 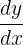
In this step, we will solve the equation for 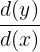 by isolating
by isolating 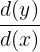 on the left hand side of the equation.
on the left hand side of the equation.
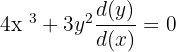
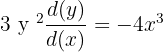
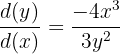
Example 2
Differentiate 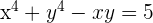
Solution
This example is trickier than the first one because two of the three terms of the function have multiple variables. The steps to differentiate this function are essentially the same.
Step 1 - Differentiate both sides of the function with respect to the variable x
We will find the derivative of each term using the rules of differentiation. On the left hand side of the equation, we will use the derivative power and product rule. On the right hand side, we will simply differentiate the constant using the derivative constant rule.
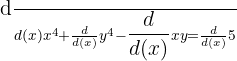
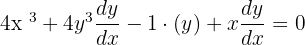
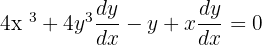
Step 2: Simplify the equation by solving for 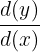
The second step involves simplification of the equation by isolating 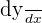 on the left hand side of the equation.
on the left hand side of the equation.
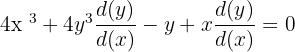
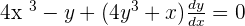


Example 3
Find the derivative of the function 
Solution
You can see that the above function involves a trigonometric sine function. The widely used trig functions are sine, cosine and tangent. Its always a good idea to memorize the derivatives of common trigonometric functions. We have also jotted down the derivatives of common trig functions at the end of this article.
Step 1 - Differentiate both sides of the function with respect to the variable x
As usual, we will find the derivative of each and every element on both sides of the function and multiply the derivative of the term with y variable by 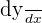 .
.

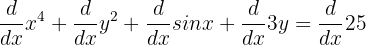
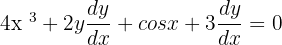
We will rewrite the equation like this:

Step 2: Simplify the equation by solving for 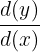
To simplify the equation we will move the terms  to the right hand side of the equation.
to the right hand side of the equation.
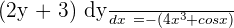
Now, we will solve the equation for 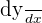 by isolating it on the left hand side:
by isolating it on the left hand side:
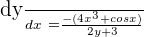
Example 4
Differentiate the function 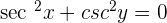
Solution
The above function is complex because it involves trigonometric functions. The procedure for differentiating this implicit function is the same as we used in the previous examples.
Step 1 - Differentiate both sides of the function with respect to the variable x
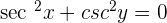
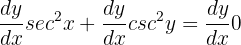
Apply the general power rule to differentiate the trig functions on the left hand side. It should be noted that the general power rule is a special kind of chain rule. The mathematical notation of this rule is given below:
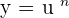
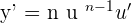
Remember that the derivative of 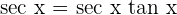 and the derivative of
and the derivative of 
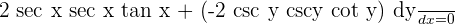
Step 2: Simplify the equation by solving for 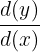
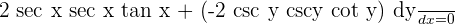
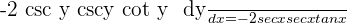

To simplify the equation further, we will cancel out the common term "-2" in the numerator and the denominator.

Derivatives of Common Trigonometric Functions
The derivatives of common trigonometric functions are given below:
Function Derivative



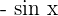


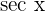


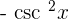
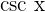
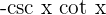
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.