Chapters
In this article, you will learn what is meant by the differential of the function and how to calculate it. Let us first see what is a differential, how to denote and compute it.

What is a Differential?
If f(x) is a differentiable function, the differential of the function corresponding to the increase of the independent variable, h, is the product f '(x) · h. It is denoted by dy.
The differential of the function depicts the main part of the change in a function y = f(x) in calculus. The change is measured with respect to the changes in the independent variable (x). You are familiar with the derivative of the function. It represents the instantaneous rate of change of the function at a given point. It is represented like this:
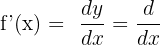
As we have mentioned earlier that the differential of the function is dy. Hence, from the above notation of the derivative, we can easily derive the formula for the differential like this:
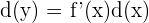
Here,  depicts the derivative of the function with respect to the independent variable x, and d(x) represents an additional real variable.
depicts the derivative of the function with respect to the independent variable x, and d(x) represents an additional real variable.
Graphically, the differential at a point represents the increase of the y-coordinate of the tangent, which corresponds to an increase in the independent variable, h.

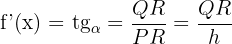
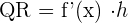 ;
; 
Example 1
Calculate the differential of the function 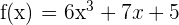 .
.
Solution
To calculate the differential, we need to find out the derivative of the above function by using the rules of the derivative. The derivative of  will be computed by using the derivative power rule. It is
will be computed by using the derivative power rule. It is  .
.
The derivative of 7x is 7 because the derivative of the constant multiplied with the variable of power 1 is equal to the constant.
The derivative of 5 is zero because the derivative of the constant is always zero.
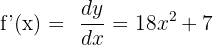
Now that we have computed the derivative of the function, we can easily calculate its differential. The formula for the differential of the function is:
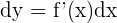
We will just substitute the value of the derivative in the above formula to get the differential:

Example 2
Calculate the differential of the function 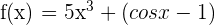 .
.
Solution
To calculate the differential, we need to find out the derivative of the above function by using the rules of derivative. The derivative of 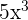 will be computed by using the derivative power rule. It is
will be computed by using the derivative power rule. It is 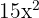 .
.
The derivative of cos x is equal to -sin x.
The derivative of -1 is zero because the derivative of the constant is always zero.
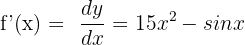
Now that we have computed the derivative of the function, we can easily calculate its differential. The formula for the differential of the function is:
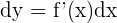
We will just substitute the value of the derivative in the above formula to get the differential:
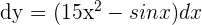
Example 3
Calculate the differential of the function 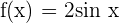
Solution
First, we will find the derivative of the above function. We know that the derivative of sin x is equal to cos x.
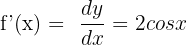
Now that we have computed the derivative of the function, we can easily calculate its differential. The formula for the differential of the function is:
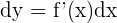
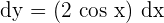
Example 4
Calculate the increase in the area of a square of 2 m² when each side is increased by 1mm.
Solution
We know that the formula for the area of the square is:
Area = Length x Length
In the context of this problem, the area is equal to  if the length of one side is x.
if the length of one side is x.
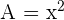
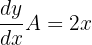
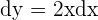
We are given that the area of the square is  , so the value of
, so the value of  . Similarly, the area of each side is increased by 1mm which is equal to 0.001 meters. This shows that the value of dx is 0.001 m. Put these values in the above formula to get the increase in the area of the square:
. Similarly, the area of each side is increased by 1mm which is equal to 0.001 meters. This shows that the value of dx is 0.001 m. Put these values in the above formula to get the increase in the area of the square:
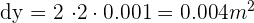
Hence, the area of the square increases by 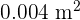 if each side is increased by 1 mm.
if each side is increased by 1 mm.
Example 5
Calculate the differential of the function  .
.
Solution
Let suppose 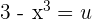 . Hence, the function will become:
. Hence, the function will become:

Apply the exponential function rule:
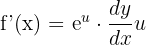
Substitute the values in the above formula to get the derivative:
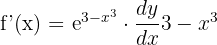
The derivative of 3 is zero because it is a constant and the derivative of  will be computed using the derivative power rule. It is
will be computed using the derivative power rule. It is 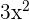 .
.
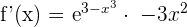
Simplifying the above answer will give us the following derivative:

Remember that we need to calculate the differential of the function, not derivative. We know that f ' (x) is equal to 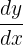 . Hence, we can easily calculate dy:
. Hence, we can easily calculate dy:
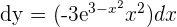
Example 6
Calculate the increase in the area of a square of 4 m² when each side is increased by 10 cm.
Solution
We know that the formula for the area of the square is:
Area = Length x Length
In the context of this problem, the area is equal to  if the length of one side is x.
if the length of one side is x.
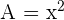
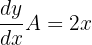
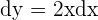
We are given that the area of the square is 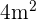 , so the value of
, so the value of  . Similarly, the area of each side is increased by 10 cm which is equal to 0.1 meters. This shows that the value of dx is 0.1 m. Put these values in the above formula to get the increase in the area of the square:
. Similarly, the area of each side is increased by 10 cm which is equal to 0.1 meters. This shows that the value of dx is 0.1 m. Put these values in the above formula to get the increase in the area of the square:

Hence, the area increases by 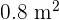 if each side is increased by 10 cm.
if each side is increased by 10 cm.
Example 7
The radius of a sphere was measured to be of 62 cm. The possibility of error in measuring its radius is no more than 0.005 cm. Find the maximum possible error in the volume of the sphere if we use this value of the radius and possible error.
Solution
The volume of the sphere is given by the following formula:
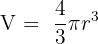
We will calculate the derivative of the function like this:
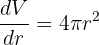
After the derivative, we can easily calculate the differential like this:
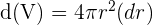
Now, we will substitute the values of radius r = 62 cm and possibility of error d(r) = 0.005 cm in the above equation to get the maximum possibility in the volume of the sphere:;



Hence, the maximum possible error in the volume of the sphere is  .
.
Summarise with AI:












Like the explanation, want to rearn more. Really enjoying the documents received.