Chapters

Introduction
Motion is rarely constant. When you drive a car, your position changes over time—this is velocity. But your velocity also changes when you speed up or slow down—this is acceleration.
In calculus, this concept of "change upon change" is handled by higher-order derivatives. Just as the first derivative tells us about the slope of a curve, subsequent derivatives reveal how that slope is changing, giving us insight into the curvature and concavity of functions.
In this article, we will explore how to calculate derivatives beyond the first, understand the notation for the nth derivative, and look at patterns that allow us to write general formulas for repeated differentiation.
Higher-Order Derivatives
The process of differentiation does not have to stop after one step. If the derivative of a function f(x) is itself a differentiable function, we can differentiate it again.
- The First Derivative, f'(x), represents the rate of change of the function.
- The Second Derivative, f''(x), is the derivative of the first derivative.
- The Third Derivative, f'''(x), is the derivative of the second derivative.
This process can continue indefinitely. These subsequent functions are called higher-order derivatives.
Notation
Mathematicians use several different notations to represent these derivatives. As the order of the derivative gets higher (like the 4th, 5th, or nth derivative), using prime marks (') becomes impractical. Instead, we use superscript numbers in parentheses or Leibniz notation.
| Derivative Order | Lagrange Notation (Primes) | Leibniz Notation (d/dx) | General Notation |
|---|---|---|---|
| First |  | 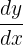 |  |
| Second | 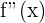 | 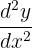 | 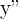 |
| Third | 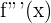 | 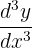 | 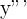 |
| Fourth | 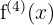 | 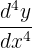 | 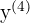 |
| nth | 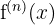 | 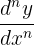 | 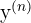 |
Nth Derivative Worked Example
Taking the derivative of a function n times results in the nth derivative.
For certain functions, a pattern emerges as we differentiate repeatedly. We can express this pattern as a general formula.
Example: Find the nth derivative of the function:
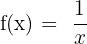
Rewrite the function using a negative exponent:
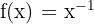
Calculate the first few derivatives to find the pattern:
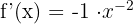
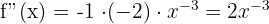
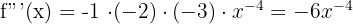
The pattern shows that the coefficient corresponds to the factorial of n (n!), and the sign alternates. The power of x is always -(n+1).
Therefore, the formula for the nth derivative is:
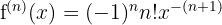
Or using fraction notation:
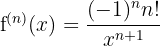
Practice Questions & Solutions
Calculate the 1st, 2nd, 3rd, and 4th derivatives of the following function:
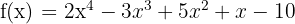
Step 1 - First Derivative.
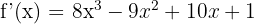
Step 2 - Second Derivative Differentiate f'(x).
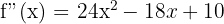
Step 3 - Third Derivative Differentiate f''(x).
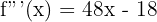
Step 4 - Fourth Derivative Differentiate f'''(x).
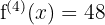
Since the result is a constant, any further derivative would be 0.
Calculate the 1st, 2nd, 3rd, 4th, and 5th derivatives of the following function:
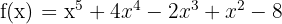
Step 1 - First Derivative
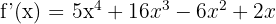
Step 2 - Second Derivative
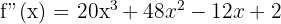
Step 3 - Third Derivative
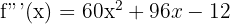
Step 4 - Fourth Derivative
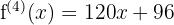
Step 5 - Fifth Derivative
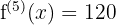
The derivative of the constant 120 is 0, so the differentiation stops changing here.
Calculate the 1st, 2nd, and 3rd derivatives of the following function:
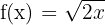
Step 1 - First Derivative: rewrite the function using a fractional exponent
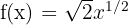
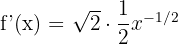
Simplify:
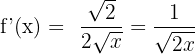
Or in exponent form for easier differentiation:
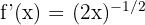
Step 2 - Second Derivative using the chain rule.
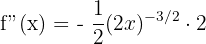
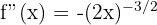
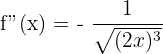
Step 3 - Third Derivative
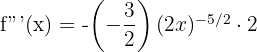
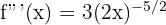
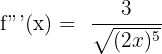
Find the 1st, 2nd, and 3rd derivatives of the following function:
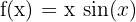
Step 1 - First Derivative - Use the Product Rule. Let u = x and v = sin(x).
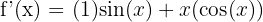
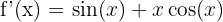
Step 2 - Second Derivative - Differentiate the result. The first term is simple; the second term (x cos(x)) requires the product rule again.
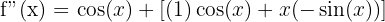
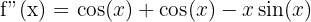
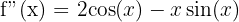
Step 3 - Third Derivative - Differentiate again.
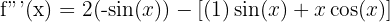

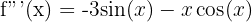
Find the 1st, 2nd, and 3rd derivatives of the function:
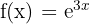
Step 1 - First Derivative - Use the Chain Rule
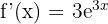
Step 2 - Second Derivative Differentiate again, multiplying by the inner derivative (3) once more.
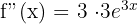
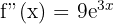
Step 3 - Third Derivative
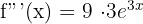
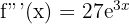
Note the pattern: the nth derivative would be:












Like the explanation, want to rearn more. Really enjoying the documents received.