Chapters

What are Derivatives?
Derivatives are one of the basic building blocks of calculus. They are defined as follows:
"An instantaneous rate of change of the function at any given point is known as derivative of that function".
The process of finding the derivative of a function is known as differentiation. When we differentiate a function, then it means that we are finding its slope. Differential calculus is a sub field of calculus. The inverse of differentiation is integration. Differentiation and integration, both are important concepts in calculus.
General Notation of the Derivative
We generally denote the derivative of the function  in the following way:
in the following way:
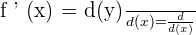
From the above notation, we can say that the derivative of the function is rate of change of y with respect to the variable x.
There are many rules of the derivatives. One of the rules is functional power rule. In this article, we will discuss the functional power rule of the derivative in detail along with relevant examples.
Derivative Power Rule
The general notation of the derivative power rule is given below:
If  , then
, then 
We can apply the power rule even if the exponent is a fraction or a negative number.
Example 1
Find derivative of the function 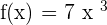 .
.
Solution
Apply the derivative power rule here by multiplying the exponent with the constant and subtracting 1 from the power of the variable.
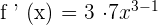
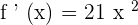
Example 2
Find derivative of the function  .
.
Solution
You can see that in the above example, the power of the function is in the fractional form. There will no impact on the differentiation of the function, if we are given fractions as an exponent. We will follow the same procedure as we followed while differentiating the functions having constants as exponents.


Example 3
Differentiate 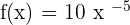
Solution
We will use the derivative power rule here by multiplying the power of the variable with the constant.

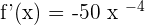
Logarithmic Differentiation
So far we have differentiated the functions in which the power of the function was a constant or a fraction. Have you ever wondered how to differentiate a function if the power of the function is a variable? Well, whenever we come across such a function, we employ logarithmic differentiation to find its derivative. Logarithmic differentiation works by taking logarithm on both sides of the function. It then uses different properties of logarithms as well as the notable logarithm chain rule to find the derivatives of functions.
Let us consider the following examples to explain this concept further.
Example 4
Differentiate 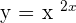 .
.
Solution
We cannot apply the derivative power rule here directly to differentiate the function because the power of one expression of the function is the variable instead of a constant. These types of functions in which the exponent or power is a variable are known as exponential functions.
To find the solution to the above exponential function, we need to apply multiple differentiation rules. For your ease, we have broken down the solution into four steps.
Step 1
First, we will apply logarithm on both sides of the function to make it a logarithmic function.

Step 2
Now, we will apply the derivative power rule as shown below:
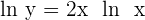
Step 3
We will use implicit differentiation here. Implicit differentiation make use of the derivative chain rule to differentiate a function.
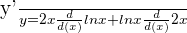
We know that if  , then
, then 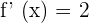 and if
and if 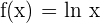 , then
, then 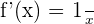 .
.
Put these values in the equation to simplify the answer:
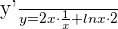
We will write the equation in the simplified form like this:
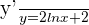
Step 4
Take y on the right hand side of the equation like this:

Substitute the value of y to get the final result:
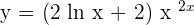
Example 5
Compute the derivative of the function 
Solution
You may be wondering if it is a differentiable function or not because the exponent is a sine function. We can easily differentiate the functions in which the exponent is a trigonometric function. The procedure is same as we used in the example 4.
Step 1
Take log on both sides of the function like this:

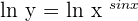
Step 2
Now, we will use the functional power rule here.

Step 3
We will use the implicit differentiation in this step.

Step 4
If 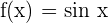 , then
, then 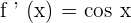 . Similarly, if
. Similarly, if 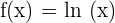 , then
, then 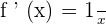 .
.

Step 5
Now, we will take on the right hand side of the equation to multiply it with the expression.
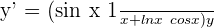
Substitute  in the equation to get the final answer:
in the equation to get the final answer:
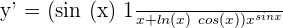
Example 6
Differentiate  .
.
Solution
Follow these steps to find the derivative of the above function.
Step 1
Take log on both sides of the equation like this:

Step 2
In this step, we will apply the derivative power rule like this:
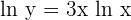
Step 3
Now, in this step, we will use implicit differentiation. Implicit differentiation means differentiating a function using the derivative chain rule.


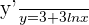
Step 4
Take y on the right hand side of the equation:
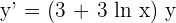
Step 5
Substitute  in the equation to get the final answer:
in the equation to get the final answer:
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.