Chapters

Introduction to Derivatives
Calculating derivatives is a fundamental concept of differential calculus. The derivative is defined as an instantaneous rate of change at a given point.
We usually differentiate two kinds of functions, implicit and explicit functions. Explicit functions are the functions in which the known value of the independent variable "x" directly leads to the value of the dependent variable "y". Implicit functions are the functions in which the known value of "x" does not directly yield the value of "y". Implicit differentiation is different than the explicit one. We use simple rules of differentiation such as product rule, power rule, quotient rule, chain rule, sum rule, and difference rule to find the derivatives of explicit functions.
Physical Interpretation of the Derivative
In this article, we will study the physical interpretation of the derivative by explaining the difference between average and instantaneous rate of change. We will also solve some of the examples related to the instantaneous rate of change. So, let's get started.
Average Velocity
We know that the derivatives represent rates of change. However, we use the word "instantaneous" whenever we are defining a derivative. You may be thinking average and instantaneous rate of change are same. However, it is not the case. Let us take an example of a velocity. The average velocity is defined below:
"The average velocity is the ratio between distance traveled (Δd) and the time elapsed (Δt)".
The formula for average velocity is given below:

The graphical representation of average velocity is given below:
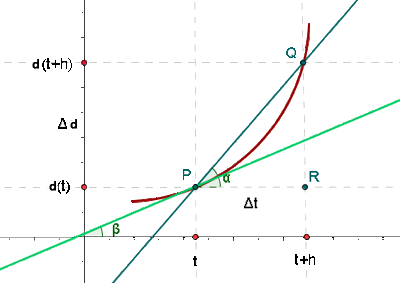
The following example will explain that average velocity is not the same as the instantaneous velocity.
Example
A car travels 90 kilometers from one city to another in 100 minutes. What is its average velocity?
Solution
The formula for average velocity = 
To convert this average speed into kilometers per hour we will multiply the average speed with 60.
= 
Thus, the average velocity or speed of the car is 54 kilometers per hour. It is the average velocity of a car during the 100 minutes of its drive. Of course, the speed of the car did not remain constant during this time frame. It kept on changing at each minute. The average velocity does not depict the rate of change at a particular point, instead, it shows the average rate of change in 100-minute time frame. Therefore, to understand what the speed or velocity of an object at a particular point was, we need to compute the instantaneous speed or velocity. In other words, we can say that average rates are different than the instantaneous rates because average rates do not depict the rates of change at a specific point.
Instantaneous Velocity
Instantaneous velocity is different than the average velocity. It is defined as:
"The instantaneous velocity is the limit of the velocity function when Δt approaches zero, that is to say, the derivative of space relative to time".
The formula for instantaneous velocity is given below:
 v(t) = \lim_(\triangle t \rightarrow 0) \frac {\triangle d} {\triangle t} = \lim _ (\triangle t \rightarrow 0) \frac {f(t + \triangle t) - f(t)} {\triangle t}
v(t) = \lim_(\triangle t \rightarrow 0) \frac {\triangle d} {\triangle t} = \lim _ (\triangle t \rightarrow 0) \frac {f(t + \triangle t) - f(t)} {\triangle t}
The graphical representation of instantaneous velocity is given below.
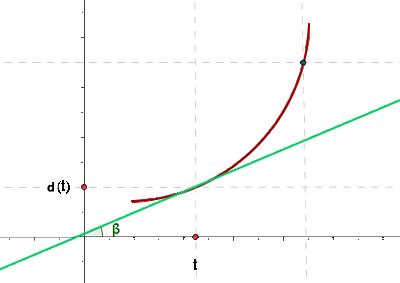
Example
The relationship between the distance traveled by car in meters and the time in minutes is given by the function 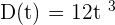 . Calculate the instantaneous velocity at t = 5 minutes.
. Calculate the instantaneous velocity at t = 5 minutes.
Solution
To compute the instantaneous velocity we need to find the derivative of the original function.

We will simplify the derivative and rewrite it as:
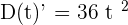
Substitute 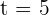 in the function to get the instantaneous velocity at
in the function to get the instantaneous velocity at 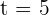 minutes:
minutes:
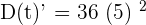
 meters per minute
meters per minute
You can see that we substituted the value of t in the derivative of the function, instead of the function itself. Hence to determine the rate of change at a specific point, we always need to differentiate the function first.
Examples of Instantaneous Rates of Change
Now, in this section, we will solve some more examples of the instantaneous rate of change.
Example 1
The position of a ball after time t in minutes is given by the following function:
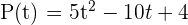
a) Is the ball moving upwards or downwards at t = 3 minutes?
b) Will the ball ever stop moving?
Solution
To answer the above question, we need to find the derivative of the original function.
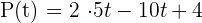

Part a
To determine whether the ball is moving upwards or downwards at t = 3 minutes, we should substitute t with 3 in the derivative of the function.

As the velocity of the ball is positive, hence we can say that the ball is moving upwards at t = 3 minutes.
Part b
To determine if the ball will stop moving or not, we need to find out the time at which the derivative of the function is equal to zero after substituting the value of t. At t = 1 minute, the derivative of the function becomes zero.
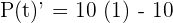
Hence, at t = 1 minute the ball is not moving.
Example 2
Suppose that the amount of water a reservoir can hold at t minutes is given by the function 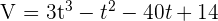 . Calculate the following.
. Calculate the following.
a) Is the volume of water in the reservoir increasing or decreasing at t = 2 minutes.
b) Is the volume of water in the reservoir increasing or decreasing at t = 4 minutes.
Solution
There are two parts of this question. To find the volume of the reservoir at a specific time interval, we need to differentiate the original function first. Differentiation means finding the derivative of a function.
Part a
The volume of the reservoir = 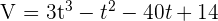
We will differentiate this volume function using the sum and power rule.
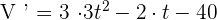
We will rewrite the above function in simplified form like this:
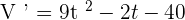
Now, we will find whether the volume of water in the reservoir was decreasing or increasing at t = 2 minutes through substitution of 2 in the derivative of the volume.
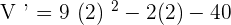
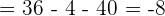
Since -8 is negative, so we can assume that the volume of the reservoir is decreasing at t = 2 minutes.
Part b
The differentiated function of the volume = 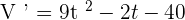
Put t = 4 in the above function to get the volume of the water in the reservoir at t = 4 minutes.
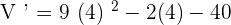
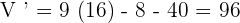
The positive rate of change shows that the volume is increasing at t = 4 minutes.













Like the explanation, want to rearn more. Really enjoying the documents received.