Chapters

Exercise 1
Differentiate the following trigonometric functions:
1 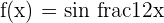
2 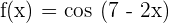
3 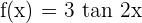
4 
5 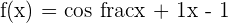
Exercise 2
Differentiate the following inverse trigonometric functions:
1 
2 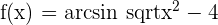
3 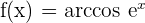
4 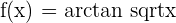
5 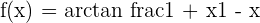
6 
Exercise 3
Differentiate the following functions using the chain rule:
1 
2 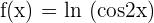
3 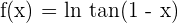
4 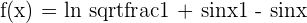
5 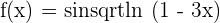
6 
7 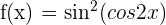
8 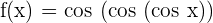
Exercise 4
Differentiate the following functions:
1 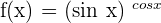
2 
Exercise 5
Find the successive derivatives:
1 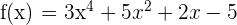
2 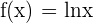
3 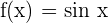
4 
Exercise 6
Differentiate the following functions:
1 
2 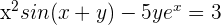
Solution of exercise 1
Differentiate the following trigonometric functions:
1 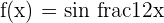
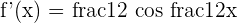
2 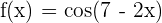
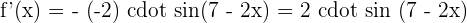
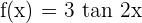
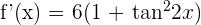

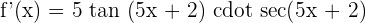
5 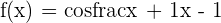
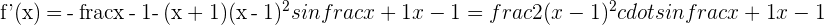
Solution of exercise 2
Differentiate the following inverse trigonometric functions:
1 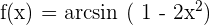
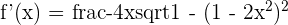
2 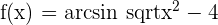

3 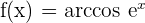
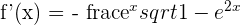
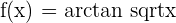
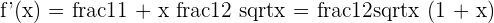
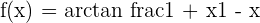
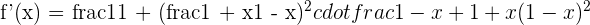
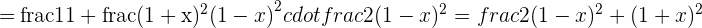
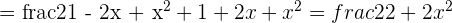
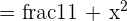
6 

= 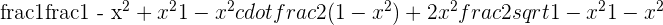

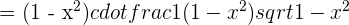
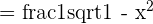
Solution of exercise 3
Differentiate the following functions using the chain rule:
1 

2 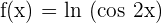
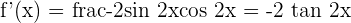
3 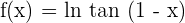
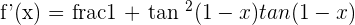
4 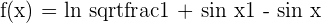

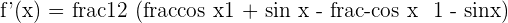

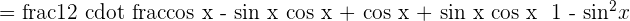
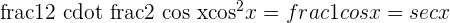
5 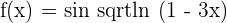
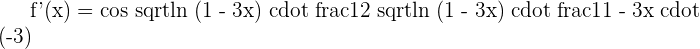

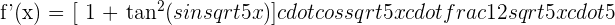
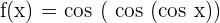

Solution of exercise 4
Differentiate the following functions:
1 
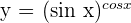

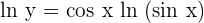

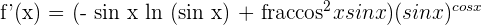
2 


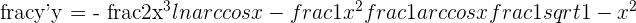
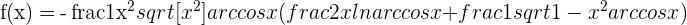
Solution of exercise 5
Find the successive derivatives:
1 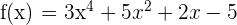
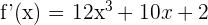
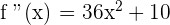
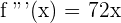
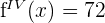

2 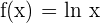

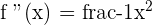


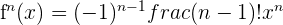
3 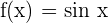


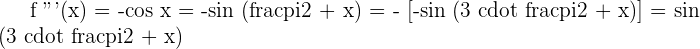
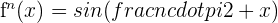
4 




Solution of exercise 6
Differentiate the following functions:
1 


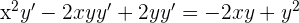

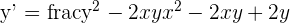
2 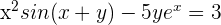
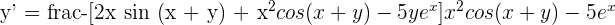
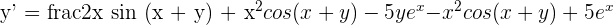
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.