Chapters

Exercise 1
Find the point in the function y = |x + 2| where it has no derivative. Justify the result by representing it graphically.
Exercise 2
Find the point in the function y = |x ² − 5x + 6| where it has no derivative. Justify the result by representing it graphically.
Exercise 3
Study the continuity and differentiability of the function defined by:
f(x) = 
Exercise 4
Given the function:

For what values of a is the function differentiable?
Exercise 5
Determine the values of a and b where the following function is continuous and differentiable:
f(x) = 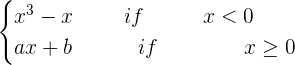
Exercise 6
Determine the values of a and b for which the function is differentiable at all points:

Exercise 7
Find the points where y = 250 − |x² −1| has no derivative.
Exercise 8
Determine for which values of a and b the function is continuous and differentiable:
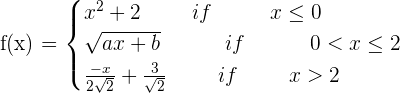
Solution of exercise 1
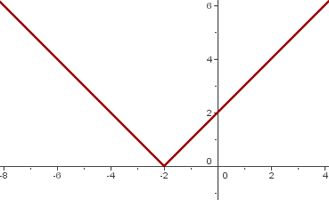
Find the point in the function y = |x + 2| where it has no derivative. Justify the result by representing it graphically.
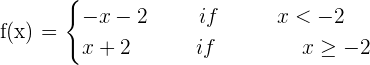
 f(-2)= \lim _ {x \rightarrow -2^{-}} f(x) = \lim _ {x \rightarrow -2^{+}} f(x)=0
f(-2)= \lim _ {x \rightarrow -2^{-}} f(x) = \lim _ {x \rightarrow -2^{+}} f(x)=0
The function is continuous.
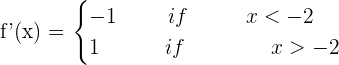
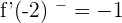
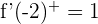
It has no derivative at P(−2,0).
Solution of exercise 2
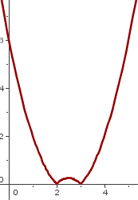
Find the point in the function y = |x ² − 5x + 6| where it has no derivative. Justify the result by representing it graphically.

 f(2)= \lim _ {x \rightarrow 2^{-}} f(x) = \lim _ {x \rightarrow 2^{+}}f(x) = 0
f(2)= \lim _ {x \rightarrow 2^{-}} f(x) = \lim _ {x \rightarrow 2^{+}}f(x) = 0
 f(3)= \lim _ {x \rightarrow 3^{-}} f(x) = \lim _ {x \rightarrow 3^{+}}f(x) = 0
f(3)= \lim _ {x \rightarrow 3^{-}} f(x) = \lim _ {x \rightarrow 3^{+}}f(x) = 0
The function is continuous.
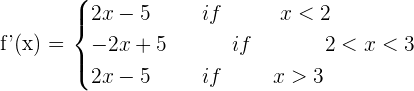
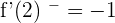
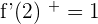

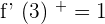
The function is not differentiable at: x = 2 and x = 3 or at points P1(2,0) and P2(3,0).
Solution of exercise 3
Study the continuity and differentiability of the function defined by:

The function is not continuous at x = 0 because it has no image. Therefore it is not differentiable.
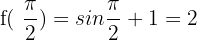
 \lim _ {x \rightarrow (\frac{\pi}{2}) ^ {-}}\frac{2x}{\pi} + 1= \lim _ {x \rightarrow (\frac{\pi}{2}) ^ {+}} sin \frac {\pi}{2} + 1 = 2
\lim _ {x \rightarrow (\frac{\pi}{2}) ^ {-}}\frac{2x}{\pi} + 1= \lim _ {x \rightarrow (\frac{\pi}{2}) ^ {+}} sin \frac {\pi}{2} + 1 = 2
 f(\frac{\pi}{2}) = \lim _ {x \rightarrow (\frac{\pi}{2})}f(x)
f(\frac{\pi}{2}) = \lim _ {x \rightarrow (\frac{\pi}{2})}f(x) 
The function is continuous.

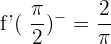
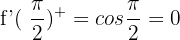
The function is not differentiable at any point.
Solution of exercise 4
Given the function:
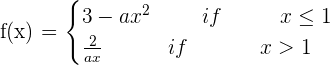
For what values of a is the function differentiable?
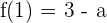
 \lim _ {x \rightarrow 1 ^ {-}}(3 - ax^2) = 3 - a
\lim _ {x \rightarrow 1 ^ {-}}(3 - ax^2) = 3 - a
 \lim _ {x \rightarrow 1 ^ {+}} \frac {2}{ax} =\frac {2}{a}
\lim _ {x \rightarrow 1 ^ {+}} \frac {2}{ax} =\frac {2}{a}


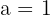

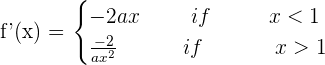
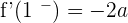
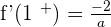
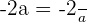


Differentiable at a = 1
For x = −1, it is not continuous.
Solution of exercise 5
Determine the values of a and b where the following function is continuous and differentiable:
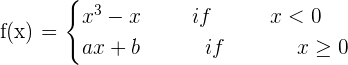

 \lim _ {x \rightarrow 0 ^ {-}}(x^3 - x) = 0
\lim _ {x \rightarrow 0 ^ {-}}(x^3 - x) = 0
 \lim _ {x \rightarrow 0 ^ {+}} (ax + b) = b
\lim _ {x \rightarrow 0 ^ {+}} (ax + b) = b

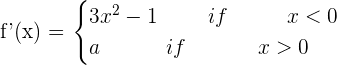
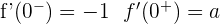
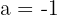
Solution of exercise 6
Determine the values of a and b for which the function is differentiable at all points:
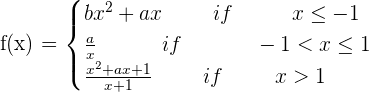
A differentiable function has to be continuous. In this case the function is not continuous for x = 0, that is to say, there are no values for a and b which make the function continuous.
Therefore, there are no values of a and b for which the function is differentiable.
Solution of exercise 7
Find the points where y = 250 − |x² −1| has no derivative.




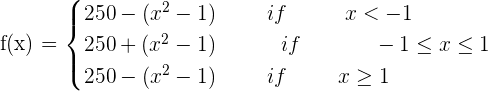

 \lim_{x\rightarrow 1 ^ {-}} 250 - (x ^2 - 1) = 250
\lim_{x\rightarrow 1 ^ {-}} 250 - (x ^2 - 1) = 250
 \lim_{x \rightarrow 1 ^ {+}} 250 + (x ^2 - 1) = 250
\lim_{x \rightarrow 1 ^ {+}} 250 + (x ^2 - 1) = 250

 \lim_{x \rightarrow 1 ^ {-}} 250 + (x^2 - 1) = 250
\lim_{x \rightarrow 1 ^ {-}} 250 + (x^2 - 1) = 250
 \lim_{x \rightarrow 1 ^ {+}} 250 - (x ^2 - 1) = 250
\lim_{x \rightarrow 1 ^ {+}} 250 - (x ^2 - 1) = 250
The function is continuous.
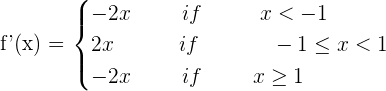
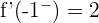

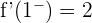
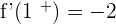
Is not differentiable at x = −1 and x = 1.
Solution of exercise 8
Determine for which values of a and b the function is continuous and differentiable:
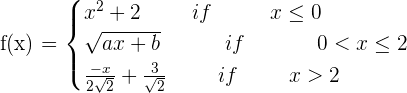
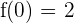
 \lim_{x \rightarrow 0^ {-}} (x ^2 + 1) = 2
\lim_{x \rightarrow 0^ {-}} (x ^2 + 1) = 2
 \lim_{x \rightarrow 0 ^{+}} \sqrt{ax + b} = \sqrt{b}
\lim_{x \rightarrow 0 ^{+}} \sqrt{ax + b} = \sqrt{b}
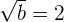

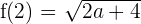
 \lim_{x \rightarrow 2 ^ {-}} \sqrt{2a + b} = \sqrt {2a + 4}
\lim_{x \rightarrow 2 ^ {-}} \sqrt{2a + b} = \sqrt {2a + 4}
 \lim_{x \rightarrow 2 ^ {+}} \frac {-2} {2 \sqrt{2}} + \frac {3} {\sqrt{2}} = \sqrt{2}
\lim_{x \rightarrow 2 ^ {+}} \frac {-2} {2 \sqrt{2}} + \frac {3} {\sqrt{2}} = \sqrt{2}
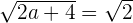
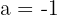
For a = −1 and b = 4, the function is continuous.
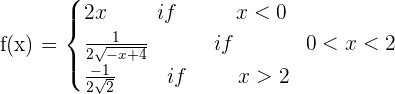

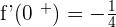
It is not differentiable at x = 0.

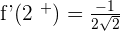
It is differentiable at x = 2.













Like the explanation, want to rearn more. Really enjoying the documents received.