Chapters

Derivative of a Function at a Point
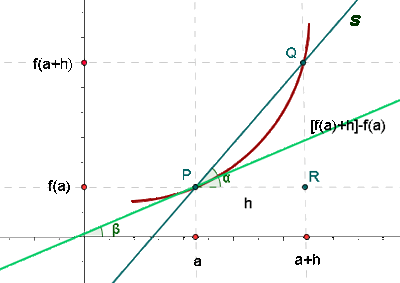
The instantaneous rate of change of a given function is the basis of calculus. It basically measures the rate of change of a function at any given point. It is similar to the concept of instantaneous velocity which measures the velocity of a moving object at a particular time interval. If we suppose that a function is an object in motion, then the instantaneous rate of change means the velocity of the object in motion.
We use the instantaneous rate of change in our real lives too. For example, we use the instantaneous rate of change when we want to measure the number of liters of petrol used by the car per day when we increase its speed at the rate of 1 kilometer per hour. We can also represent an instantaneous rate of change graphically.
Using the Limit Formula to Calculate the Derivative of a Function
Do you know we can use the limit formula to calculate the derivative of a function, instead of applying the rules of derivatives directly on a given function? The derivative of the function f(x) at x = a is the value of the limit, if it exists at this point when the variable, h, tends to zero. Consider the function f, whose instantaneous rate of change at an interval (a, a+h) is denoted by the following formula:
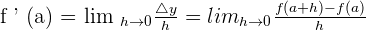
In this article, we will see how to calculate the derivatives of the functions using the above formula. Let us proceed to some examples which will make you understand how to use the above formula to calculate derivatives.
Example 1
Find the derivative of the function 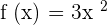 at
at  .
.
Solution
Use the formula 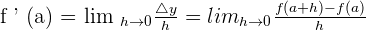 to solve this example:
to solve this example:
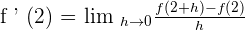
As the function is 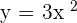 , hence we will take the square of the functions in the numerator like this:
, hence we will take the square of the functions in the numerator like this:

Apply the formula  to solve the terms inside the brackets in the numerator:
to solve the terms inside the brackets in the numerator:

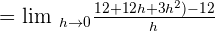

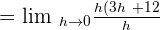

Now, substitute  in the above equation to get the limit of the original function:
in the above equation to get the limit of the original function:
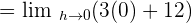

Example 2
Use the limit formula to calculate the derivative of  .
.
Solution
We will use the following limit formula to compute the derivative:
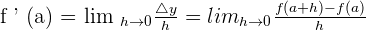
In this example,. 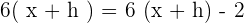 and
and 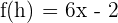 .
.
Put these values in the limit formula of the derivative:

Solve the expression by opening the parenthesis in the numerator:
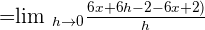

H in the numerator and the denominator will be cancelled out. The resultant function will be:
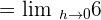
Example 3
Use the limit formula to compute the derivative of the following function:
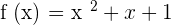
Solution
The limit formula to compute the derivative of the function is:
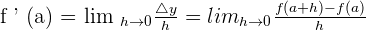
Here, 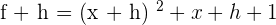 and
and 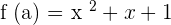 .
.
Put the above values in the formula:
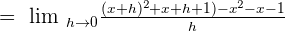
Use the formula  to expand the square term in the above expression:
to expand the square term in the above expression:
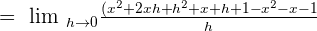
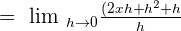
H is the common term in the numerator and the denominator, hence we will cancel it out like this:
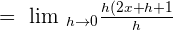
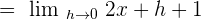
Plug  in the above expression to get the limit of the original function:
in the above expression to get the limit of the original function:
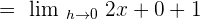
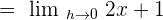
Example 4
Use the limit formula to calculate the derivative of the following function:
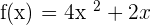
Solution
Use the formula 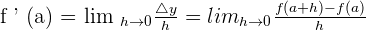 to calculate the derivative:
to calculate the derivative:
Here,  and
and 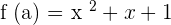
Putting the above values in the formula we will get the following expression:
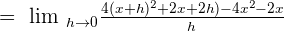
Use the formula  to expand the square term in the above expression:
to expand the square term in the above expression:


Like terms with opposite signs will be cancelled out:
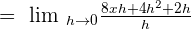
h is the common term in both the numerator and the denominator. Hence, we will cancel it out to get the following expression:
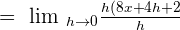
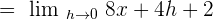
Plug  in the above equation to get the value of the derivative of the original function:
in the above equation to get the value of the derivative of the original function:
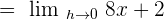
Example 5
Find the derivative of the following function using the limit formula:

Solution
Use the formula 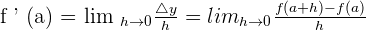 to calculate the derivative:
to calculate the derivative:
Here,  and
and 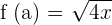
Putting the above values in the formula we will get the following expression:

Since, we have got the minus sign in the middle of the two terms in the numerator of the above function, so we will solve the remaining example by multiplying the term in the numerator by its conjugate:


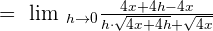

h in the numerator and the denominator will be cancelled out. Hence, the resulting expression will be:

Put h = 0 in the above expression to get the limit of the original function:
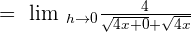
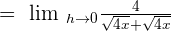
We know that 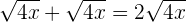 :
:
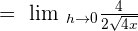
Put 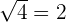 in the above expression:
in the above expression:

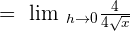
4 in the numerator and the denominator will be cancelled out. Hence, the limit of the original function is:
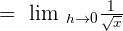
Example 6
Find the derivative of the following function using the limit formula:
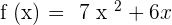
Solution
Use the formula 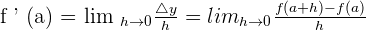 to calculate the derivative:
to calculate the derivative:
Here,  and
and 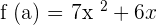
Putting the above values in the formula we will get the following expression:
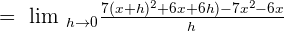
Use the formula  to expand the square term in the above expression:
to expand the square term in the above expression:
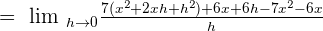
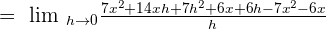
Like terms with opposite signs will be cancelled out:
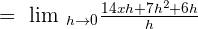
h is the common term in both the numerator and the denominator. Hence, we will cancel it out to get the following expression:
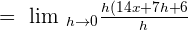

Plug  in the above equation to get the value of the derivative of the original function:
in the above equation to get the value of the derivative of the original function:
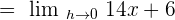
Example 7

Solution
Use the formula 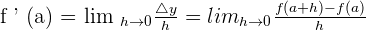 to calculate the derivative:
to calculate the derivative:
Here, 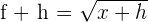 and
and 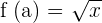
Putting the above values in the formula we will get the following expression:
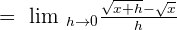
Since, we have got the minus sign in the middle of the two terms in the numerator of the above function, so we will solve the remaining example by multiplying the term in the numerator by its conjugate:
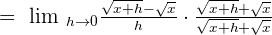
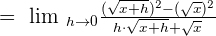
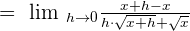
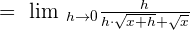
h in the numerator and the denominator will be cancelled out. Hence, the resulting expression will be:
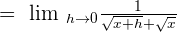
Put h = 0 in the above expression to get the limit of the original function:
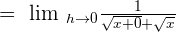
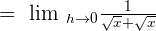
We know that 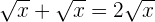 :
:
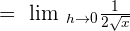
Example 8
Use the limit formula to calculate the derivative of the following function:

Solution
Use the formula 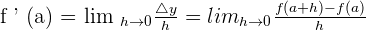 to calculate the derivative:
to calculate the derivative:
Here,  and
and 
Putting the above values in the formula we will get the following expression:
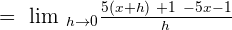

Like terms with opposite signs will be cancelled out:

h is the common term in both the numerator and the denominator. Hence, we will cancel it out to get the following expression:

Example 9
Use the limit formula to calculate the derivative of the following function:
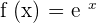
Solution
Use the following limit formula to calculate the derivative of the above function:
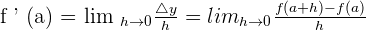
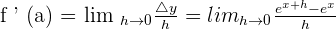

Using the graphing calculator we can find the value of  :
:
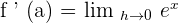
Hence, the derivative of  =
= 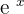 .
.













Like the explanation, want to rearn more. Really enjoying the documents received.