Chapters

Introduction
The fundamental theorem of calculus refers to a theorem that associates the concept of differentiation with the concept of integration of a function. This theorem has two parts. The first part of the theorem is also referred to as the first fundamental theorem of calculus. According to this part of the theorem, one of the antiderivatives or indefinite integral, for example, F, of a function f may be calculated as the integral of f with a variable bound of integration. It points out the fact that the antiderivatives of the continuous functions exist.
On the other hand, according to the second part of the theorem which is also known as second fundamental theorem of calculus, says that the integral of any function f over some interval can be calculated by using anyone, for example, F, of its infinite antiderivatives.
If we have to summarize the above discussion, we can say that the fundamental theorem of calculus implies the relationship between differentiation and integration. Sir Isaac Newton and Gottfried Wilhelm Leibenz discovered this relationship in 1600s and early 1700s. The term fundamental shows that how important this theorem is in the entire development of calculus.
Mathematical Notation
According to the first part of the fundamental theorem of calculus, is f is continuous on the close interval [a, b], and F is the indefinite integral of f on closed interval [a, b], then:

The second part of fundamental theorem of calculus says that for a continuous function f on an open interval I, any point a in I, and if F is defined by:
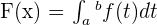
Then:
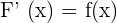
at each point in I.
In the next section, we will solve some examples which will make this concept more clear.
Example 1
Calculate the definite integral of the following function:

Solution
First, we need to find the antiderivative of the function  . The antiderivative of this function is
. The antiderivative of this function is 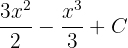 . For your ease choose C = 0.
. For your ease choose C = 0.
According to the fundamental theorem of calculus:


Substitute 3 and 0 in the antiderivative of the function:
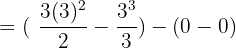
= 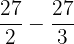
= 
Example 2
Calculate the definite integral of the following function:
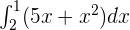
Solution
First, we need to find the antiderivative of the function  . The antiderivative of this function is
. The antiderivative of this function is 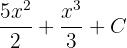 . For your ease choose C = 0.
. For your ease choose C = 0.
According to the fundamental theorem of calculus:

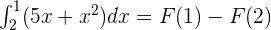
Substitute 1 and 2 in the antiderivative of the function:
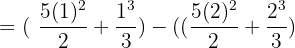
= 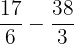
= 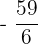
Example 3
Calculate the definite integral of the following function:
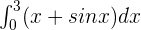
Solution
First, we need to find the antiderivative of the function 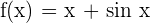 . The antiderivative of this function is
. The antiderivative of this function is 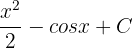 . For your ease, choose C = 0.
. For your ease, choose C = 0.
According to the fundamental theorem of calculus:

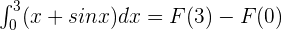
Substitute 3 and 0 in the antiderivative of the function:
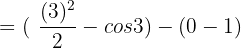
= 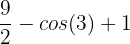
= 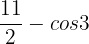
Example 4
Calculate the definite integral of the following function:

Solution
First, we need to find the antiderivative of the function 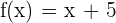 . The antiderivative of this function is
. The antiderivative of this function is 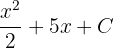 . For your ease choose C = 0.
. For your ease choose C = 0.
According to the fundamental theorem of calculus:


Substitute 3 and 0 in the antiderivative of the function:
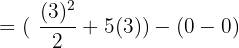
= 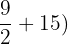
= 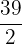
Example 5
Calculate the definite integral of the following function:

Solution
First, we need to find the antiderivative of the function 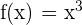 . The antiderivative of this function is
. The antiderivative of this function is 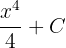 . For your ease choose C = 0.
. For your ease choose C = 0.
According to the fundamental theorem of calculus:


Substitute 1 and -1 in the antiderivative of the function:
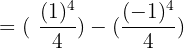

=
Example 6
Calculate the definite integral of the following function:
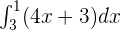
Solution
First, we need to find the antiderivative of the function  . The antiderivative of this function is
. The antiderivative of this function is  . For your ease choose C = 0.
. For your ease choose C = 0.
According to the fundamental theorem of calculus:

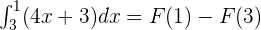
Substitute 1 and 3 in the antiderivative of the function:
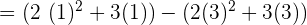
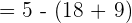
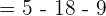
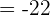
Example 7
Calculate the definite integral of the following function:
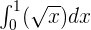
Solution
First, we need to find the antiderivative of the function  . The antiderivative of this function is
. The antiderivative of this function is 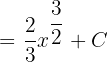 . For your ease choose C = 0.
. For your ease choose C = 0.
According to the fundamental theorem of calculus:

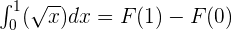
Substitute 1 and 0 in the antiderivative of the function:
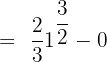
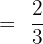
Example 8
Calculate the definite integral of the following function:

Solution
First, we need to find the antiderivative of the function 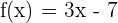 . The antiderivative of this function is
. The antiderivative of this function is 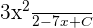 . For your ease choose C = 0.
. For your ease choose C = 0.
According to the fundamental theorem of calculus:

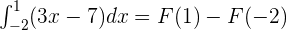
Substitute 1 and -2 in the antiderivative of the function:
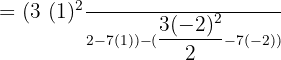

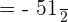
Example 9
Calculate the definite integral of the following function:

Solution
First, we need to find the antiderivative of the function 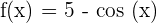 . The antiderivative of this function is
. The antiderivative of this function is 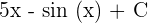 . For your ease choose C = 0.
. For your ease choose C = 0.
According to the fundamental theorem of calculus:

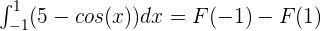
Substitute 1 and -1 in the antiderivative of the function:
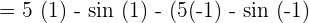
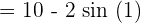
Example 10
Calculate the definite integral of the following function:

Solution
First, we need to find the antiderivative of the function 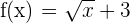 . The antiderivative of this function is
. The antiderivative of this function is 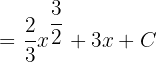 . For your ease choose C = 0.
. For your ease choose C = 0.
According to the fundamental theorem of calculus:

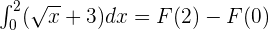
Substitute 2 and 0 in the antiderivative of the function:
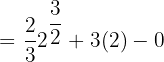
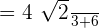












Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,