Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
Exercise 1
Study the following functions and determine if they are continuous. If not, state where the discontinuities exist and what type they are:
1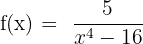 
2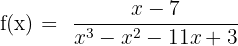 
3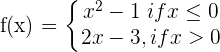 
4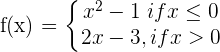 
5 
6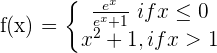 
Exercise 2
Determine if the following function is continuous at x = 0.
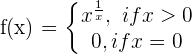
Exercise 3
Determine if the following function is continuous on (0,3). If not, state where the discontinuities exist and what type they are:
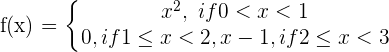
Exercise 4
Are the following functions continuous at x = 0?
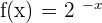
Exercise 5
Given the function:
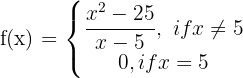
1 Prove that f(x) is not continuous at x = 5.
2Is there a continuous function which coincides with f(x) for all values with the exception x = 5? If so, determine the function.
Exercise 6
Determine if the following function is continuous. If not, state where the discontinuities exist or why the function is not continuous:
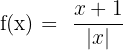
Exercise 7
Determine if the following function is continuous at x = 0.
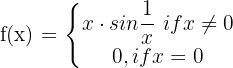
Exercise 8
Determine the value of a to make the following function continuous.
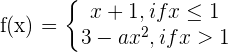
Exercise 9
The function defined by:
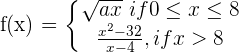
is continuous on [0, ∞).
Determine the value of a that would make this statement true.
Solution of exercise 1
Study the following functions and determine if they are continuous. If not, state where the discontinuities exist:
1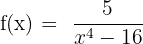
The function is continuous at all points of its domain.
D = R − {−2,2}
The function has two points of discontinuity at x = −2 and x = 2.
2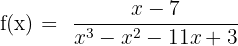
The function is continuous at R with the exception of the values that annul the denominator. If this is equal to zero and the equation is solved, the discontinuity points will be obtained.
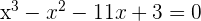
x = −3; and by solving the quadratic equation: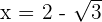 
and 
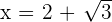are also obtained
The function has three points of discontinuity at 
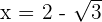, and .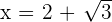
3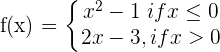
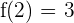
\lim _ {x \rightarrow 2^{-}} (x + 1) = 3
\lim _ {x \rightarrow 2^{+}} (2x - 1) = 3
The function is continuous.
4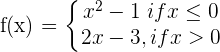
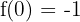
\lim _ {x \rightarrow 0^{-}} (x^2 - 1) = -1
\lim _ {x \rightarrow 0^{+}} (2x - 3) = -3
The function has a jump discontinuity at x = 0 .
5
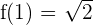
\lim_{x \rightarrow 1^{-}} (\frac{1}{x}) = 1
\lim_{x \rightarrow 1^{+}} \sqrt{x + 1} = \sqrt{2}
The function has a jump discontinuity at x = 1 .
6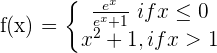
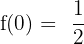
\lim_{x \rightarrow 0^{-}} (\frac {e^x}{e^x + 1}) = \frac{1}{2}
\lim_{x \rightarrow 0^{+}} x^2 + 1 = 1
The function has a jump discontinuity at x = 1/2 .
Solution of exercise 2
Determine if the following function is continuous at x = 0.
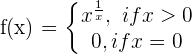
\lim_{x \rightarrow 0^{+}} x^ {\frac{1}{x}} = 0 ^ {\frac{1}{0^{+}}} = 0 ^{\infty} = 0
\lim_{x \rightarrow 0^{-}} x^ {\frac{1}{x}}
At x = 0, there is an essential discontinuity.
Solution of exercise 3
Determine if the following function is continuous on (0,3). If not, state where the discontinuities exist and what type they are:
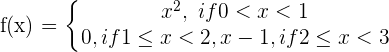
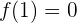
\lim_{x \rightarrow 1^{-}} x^2 = 1
\lim_{x \rightarrow 1^{+}} 0 = 0
At x = 1, there is a jump discontinuity.
\lim_{x \rightarrow 2^{-}} 0 = 0
\lim_{x \rightarrow 2^{+}} x - 1 = 1
At x = 2, there is a jump discontinuity.
Solution of exercise 4
Are the following functions continuous at x = 0?
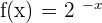
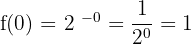
\lim_{x \rightarrow 0^{-}} 2^{-x} = 2 ^{0^{-}} = 2^0 = 1
\lim_{x \rightarrow 0^{+}} 2^{-x} = 2^{-0^{+}} = \frac{1}{2^0} = 1
The function is continuous at x = 0.
Solution of exercise 5
Given the function:
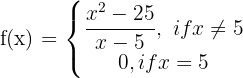
1 Prove that f(x) is not continuous at x = 5.
\lim_{x \rightarrow 5} \frac{x^2 - 25}{x - 5} = \frac{0}{0}
Solve the indeterminate form.
\lim_{x \rightarrow 5} \frac{(x + 5) (x - 5)}{x - 5} = \lim_{x \rightarrow 5} (x + 5) = 10
f (x) is not continuous at x = 5 because:
\lim_{x \rightarrow 5} f(x) \neq f(5)
2 Is there a continuous function which coincides with f(x) for all values with the exception x = 5? If so, determine the function.
If \lim_{x \rightarrow 5} f(x) = f(5) = 10 the function would be continuous, then the function is redefined:
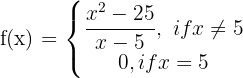
Solution of exercise 6
Determine if the following function is continuous. If not, state where the discontinuities exist or why the function is not continuous:
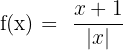
The function f(x) is continuous for x ≠ 0. Therefore, study the continuity at x = 0.
\lim_{x \rightarrow 0 ^{-}} \frac{x + 1}{|x|} = \lim_{x \rightarrow 0^{-}} \frac{x + 1}{-x} = \lim_{x \rightarrow 0^{-}}(-1 - \frac{1}{x}) = -1 - \frac{1}{0^{-}} = \infty
\lim_{x \rightarrow 0 ^{+}} \frac{x + 1}{|x|} = \lim_{x \rightarrow 0^{+}} \frac{x + 1}{x} = \lim_{x \rightarrow 0^{+}}(-1 - \frac{1}{x}) = -1 - \frac{1}{0^{+}} = \infty
The function is not continuous at x = 0, because it is defined at that point.
Solution of exercise 7
Determine if the following function is continuous at x = 0:
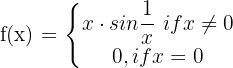
The function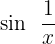 
is bounded by 
, 
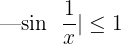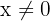, therefore takes place:
\lim_{x \rightarrow{0}} (x \cdot sin \dfrac{1}{x}) = 0, since any number multiplied by zero gives zero.
As f(0) = 0.
The function is continuous.
Solution of exercise 8
Determine the value of a to make the following function continuous:
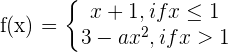
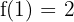
\lim_{x \rightarrow 1^{-}} (x + 1) = 2
\lim_{x \rightarrow 1^{+}} (3 - ax^2) = 3 - a
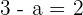
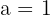
Solution of exercise 9
The function defined by:
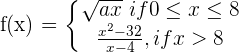
is continuous on [0, ∞).
Determine the value of a that would make this statement true.
\lim_{x \rightarrow 8^{-}} \sqrt{ax} = \sqrt{8a}
\lim_{x \rightarrow 8^ {+}} \frac{x^2 - 32}{x - 4} = 8
Did you like this article? Rate it!
Loading...
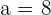
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice