
Domain of a Function
Functions provide different answers on different input values. This is important to note that we need to consider things that are physically possible, unlike imaginary numbers. For example, a ticket costs  dollars, you want to buy all your friends the ticket since it is your birthday. Let's say you have
dollars, you want to buy all your friends the ticket since it is your birthday. Let's say you have  friends and that means the total cost will be
friends and that means the total cost will be 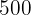 dollars. What just happened right now? How you figured that it will cost that much? Basically, you made a function which is
dollars. What just happened right now? How you figured that it will cost that much? Basically, you made a function which is 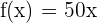 and since the value of x is
and since the value of x is  hence,
hence, 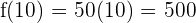 . In other words, if you input
. In other words, if you input  in the function, it will give you
in the function, it will give you 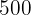 . Hence, the value of
. Hence, the value of  gives an answer that will be different from other answers. Although, this isn't something to consider inevitable. That is why mathematicians introduce a new concept of domain and range of a function.
gives an answer that will be different from other answers. Although, this isn't something to consider inevitable. That is why mathematicians introduce a new concept of domain and range of a function.
Basically, the domain is the set of elements that has an image. Although the image is a very generic word, in the mathematics world we call it range. Let's take an example below:
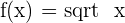
D = {x

Initial set Final set
Domain Range
The left oval represents the domains of the function and on right are the ranges of the function. You might be wondering why there is no image of  ? That is because it will result in an imaginary number. Hence, we can conclude that the domain of a function is an independent variable, however, the range is the dependent variable. The range shows what you can expect from a function.
? That is because it will result in an imaginary number. Hence, we can conclude that the domain of a function is an independent variable, however, the range is the dependent variable. The range shows what you can expect from a function.
Different Types of Domains for Different Function
For every function, there can be different domains as well as ranges. Let's talk about them in detail.
Domain of a Polynomial Function
The domain is R.

Domain of a Rational Function
The domain is R, minus the values that would annul the denominator (there cannot be a number whose denominator is zero).
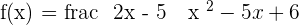

Domain of an Irrational Function of Odd Index
The domain is R.

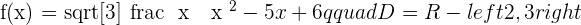
Domain of an Irrational Function of Even Index
The domain is formed by all the values that make the radicand greater than or equal to zero.

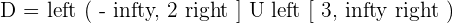
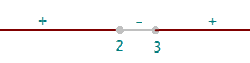

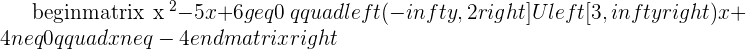

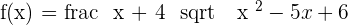
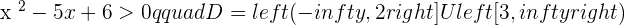

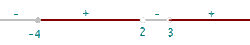
Domain of a Logarithmic Function
The domain is formed by all the values that make the inside of the logarithmic greater than zero.
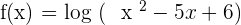
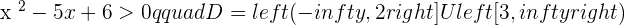
Domain of an Exponential Function
The domain is R.
Domain of the Sine function
The domain is R.
Domain of a Cosine function
The domain is R.
Domain of a Tangent Function
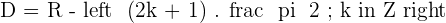

Domain of a Cotangent Function
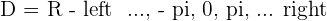
Domain of a Secant Function
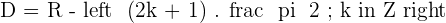

Domain of a Cosecant Function
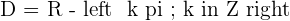
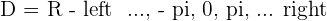
Domain of Operations with Functions
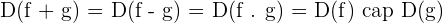

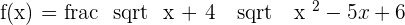

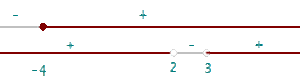
Solved the system of Inequalities.
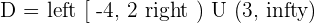











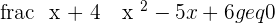



I have math qstn problm
Break even point