Chapters

Probability
| Definition | Notation | Example | |
| Random Variable | A variable whose outcomes are unknown | X,Y,A,B,etc. | A coin toss: C |
| Sample Space | All possible outcomes of the variable | S = {} | S = {H,T} |
| Event | An outcome or combination of outcomes | E = (any outcome of a random variable) | E = H |
While this may seem confusing, it may be helpful to illustrate the concepts.
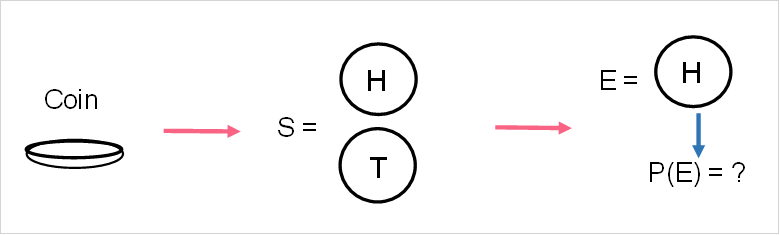
In the picture above, we can see the random variable of a coin toss represented by C. There are only 2 possible outcomes, making up the sample space. As an event, we have chosen landing on H. Now what is the probability of this event occurring? It is defined as the likelihood of an event.
Probability Distribution
Probability distributions are visualizations that illustrate all of the possible outcomes of a random variable, along with the probabilities of those outcomes occurring. To illustrate this, take a look at the probability of landing on heads if we flip the coin 3 times.

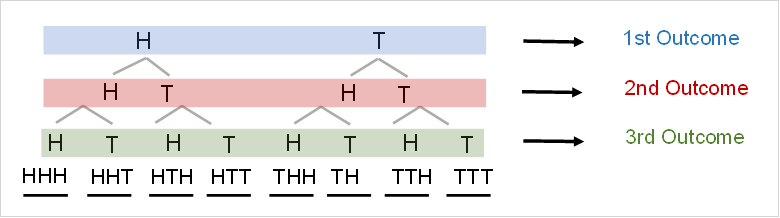
When we flip the coin once, we only have two possibilities: heads and tails. However, flipping the coin two times gives us four possibilities. If we continued to flip the coin, we would get even more!
| Flip | Outcomes | Probability of H |
| 1 | H T | P(0) = 1/2 P(1) = 1/2 |
| 2 | HH HT TH TT | P(0) = 1/4 P(1) = 2/4 P(2) = 1/4 |
| 3 | HHH HHT HTH HTT THH THT TTH TTT | P(0) = 1/8 P(1) = 3/8 P(2) = 3/8 P(3) = 1/8 |
Instead of always writing out every probability when we flip a coin, we can simply use a probability distribution. Because the properties of distributions never change, we can use probability equations to find the probability rather than by hand.
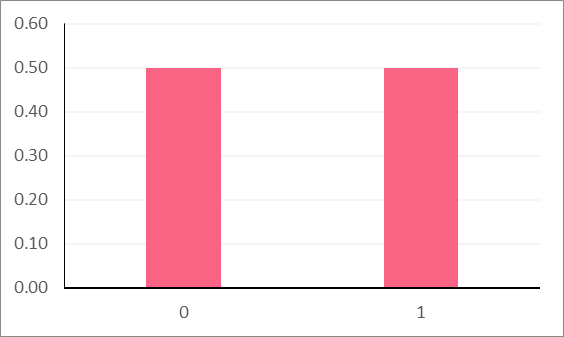
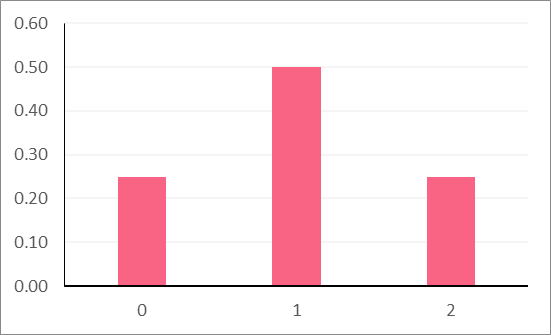

Types of Distributions
There are a couple of common distributions that you can use to calculate the probability of a random event. While the parameters of these distributions may change from situation to situation, the underlying properties of the distribution don’t. Take a look at three common distributions: normal, poisson and binomial.
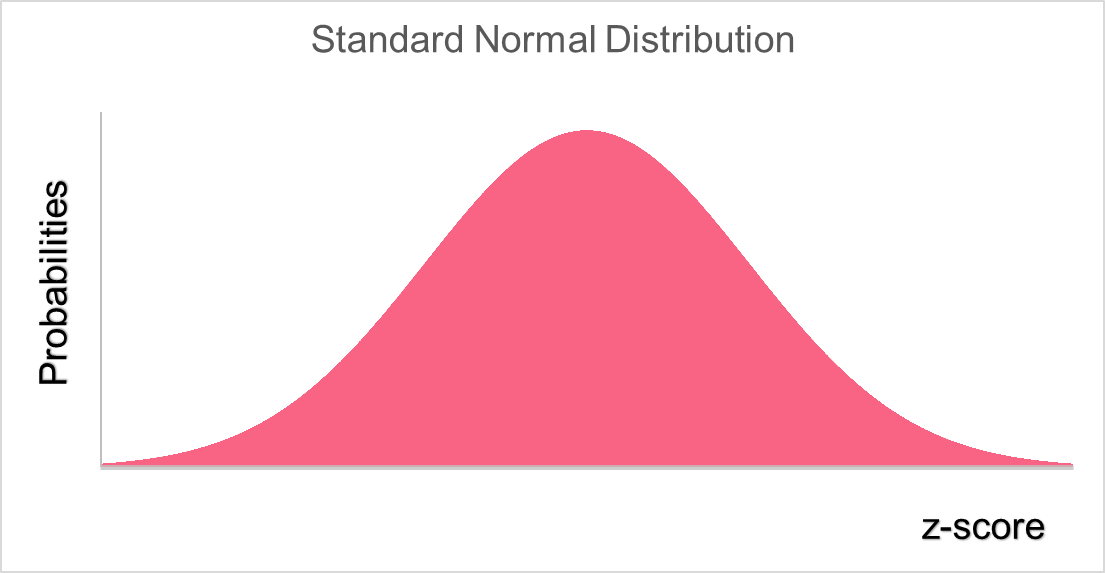


The notation above can be explained by the table below.
| Parameters | Use When | Probability | ||
| Normal | X~N(0,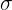 ) ) | Mean = 0 SD = | X is normally distributed | z = 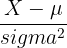 |
| Poisson | X~P(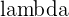 ) ) | 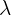 = average times x occurs per interval = average times x occurs per interval | When X is in an interval (time, space, etc) | 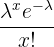 |
| Binomial | X~B(n,p) | p = number of successes q = number of failures n = number of trials | When X has only two outcomes |  |
Binomial Distribution Properties
As you can see above, each distribution has its own parameters. Let’s focus on the binomial distribution. Binomial distributions model random variables that have only two outcomes, which are balled binary outcomes or Bernoulli trials. The image below shows some examples.

For binomial distributions, we are looking for the probability of betting x number of successes in n Bernoulli trials. In other words, if we have 15 people taking an exam, what is the probability that 3 of them will pass? In this example, the parameters would be the following.
| Description | |
| X = x | 3 people passing the exam |
| n | 15 people (which we can think of as trials) |
| p | The probability of someone passing |
| q | The probability of someone failing, which is just 1 - p |
Binomial Probability Example
Let’s continue with the example in the previous section. In this case, the exam has only two outcomes: pass or fail. From all the previous years, we know that the probability of passing the exam is 60%, which means that the probability of failing the exam is 40%.
The reason why we can write q=1-p is simple. Say you have 10 students and you know that 6 have passed. Because we know 6 have passed, that means the remaining 4 have had to fail as that is the only other option.
In order to solve our example, where we want to know the probability of exactly 3 people passing out of 15 students, we simply need to plug it into the equation. Keep in mind that the equation for a combination is the following:


This will give us the following.
 | 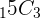 | 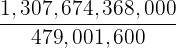 = 455 = 455 |
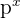 | 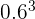 | 0.216 |
 | 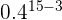 | 0.000017 |
Finally, we simply plug in the values into the formula.
\[
455*0.216*0.000017 = 0.001649 = 0.16%
\]
Problem 1
You are interested in knowing what the probability is of landing on heads 5 times when tossing a coin 10 times. Name what distribution you would use here. Justify your reasoning with an explanation on why you would choose that particular distribution.
Solution 1
In this scenario, you could use a binomial distribution. This is because tossing a coin is a random variable that only has two outcomes: heads or tails. This is a binary outcome, which you can also call Bernoulli trials.
Problem 2
Continuing with problem one, we want to find the probability using what we know about the binomial distribution. State what each parameter would be here.
Solution 2
The parameters for this problem are listed below. Because it’s a coin toss, there is always a 50% chance of landing on heads.
| Value | |
| n | 10 |
| x | 5 |
| p | 0.5 |
| q | 0.5 |
Problem 3
Using what you’ve found so far, find the probability for the scenario in problem 1 using the information about binomial distributions.
Solution 3
We simply need to plug in the information into the formula.
\[
\frac{3,628,800}{120*120} * 0.5^{5} * 0.5^{10-5} = 0.2461 = 25%
\]
Summarise with AI:













