Chapters

What is Probability Theory
Statistics is almost always introduced to students through a course in probability. This is because for many subjects within the discipline of statistics, the concepts within often involve some form of probability. Probability theory is quite simply a field within maths that deal with probability.
In order to understand probability, there are a few basic terms that one must understand. These terms are listed in the table below, along with their definitions. These terms form the building blocks for some of the more complex notions of probability.
| Concept | Definition |
| Random Variable | A variable whose outcome is unknown |
| Sample Space | All possible outcomes of a random variable |
| Probability | The chance of one outcome out of the sample space occurring |
Probability Distributions
To start to unpack what a probability distribution is, it can be helpful to start with some basic notions in statistics. First, let’s start with the concepts of frequency and a frequency distribution, whose definitions can be found in the table below.
| Concept | Definition | Example |
| Frequency | How often a value within a variable occurs | The colour blue occurs 14 times in a set of marbles |
| Frequency Distribution | Displays how often each value occurs within a variable | A bar chart showing how many marbles of each colour there are in a set |
To give you an idea of how frequency is calculated, take the data set below as an example.
| Number | Colour |
| 1 | Red |
| 2 | Blue |
| 3 | Green |
| 4 | Green |
| 5 | Red |
| 6 | Green |
In order to calculate the frequency of the colours included in this marble set, you simply need to count the amount of times each colour occurs. This would lead to the following result.
| Colour | Frequency | Frequency in % |
| Red | 2 | 33% |
| Blue | 3 | 50% |
| Green | 1 | 17% |
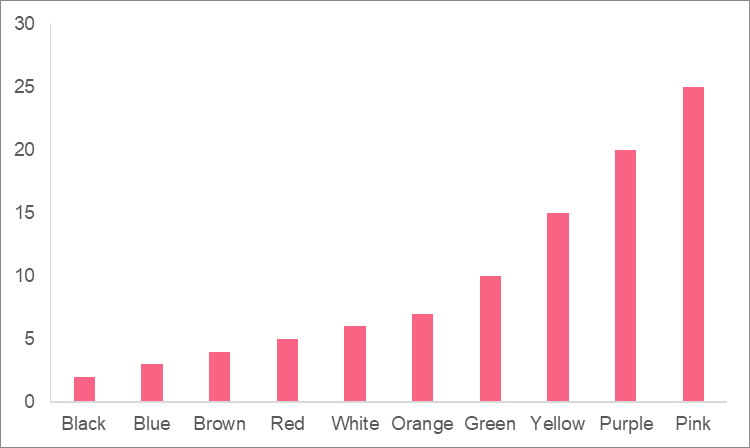
Now, let’s see how this relates to a frequency distribution. Let’s continue this example of a set of marbles and take a look at a data set containing ten different colours of marbles. The frequencies for each colour have already been calculated.
| Colour | Frequency |
| Red | 5 |
| Blue | 3 |
| Green | 10 |
| Orange | 7 |
| Yellow | 15 |
| Black | 2 |
| Purple | 20 |
| White | 6 |
| Pink | 25 |
| Brown | 4 |
In order to get a better understanding of the data, we could plot this information onto a bar chart, like the one below. Doing this gives us a frequency distribution. A frequency distribution is simply a function, or a visualization, that shows how often a given value occurs for one variable. In this case, the frequency distribution tells us how often each different colour occurs within the variable of marble colour.
Probability distribution
A probability distribution is the extension of a frequency distribution. This is because the underlying concepts for both of these measures are the same. The table below gives a brief definition of probability and probability distributions.
| Definition | Example | |
| Probability | The likelihood of an event | In the sample space S={H,T}, which is heads and tails, the probability of the event H (heads) is 0.50 |
| Probability Distribution | Formula or visual representation of the probability of each outcome in the sample space | The probability distribution would follow a binomial distribution |
To give you an idea of how probability distributions are created, let’s continue with the example of a coin toss. Say that you would like to see the probability distribution of landing on heads if you flip a coin 5 times. First, determine all the possible outcomes.
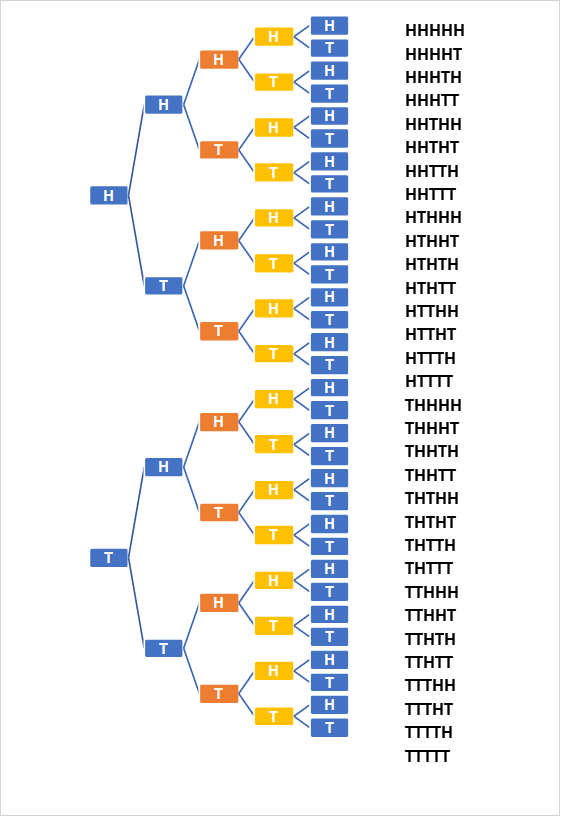
In order to get the probability of landing on heads 0-5 times, you simply divide the events over the total possible outcomes. Drawing this out onto a probability distribution, we get the following.
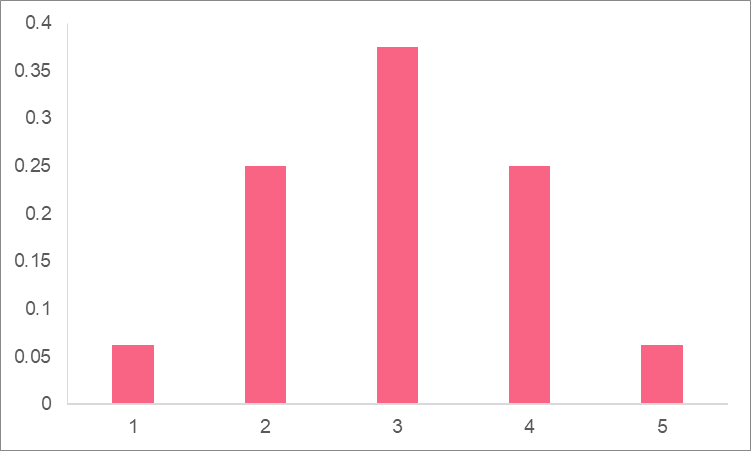
Standard Normal Distribution Problem
Recall that knowing a variable’s probability distribution means we can perform hypothesis tests on the variable. Standard normal distribution is the following probability distribution.
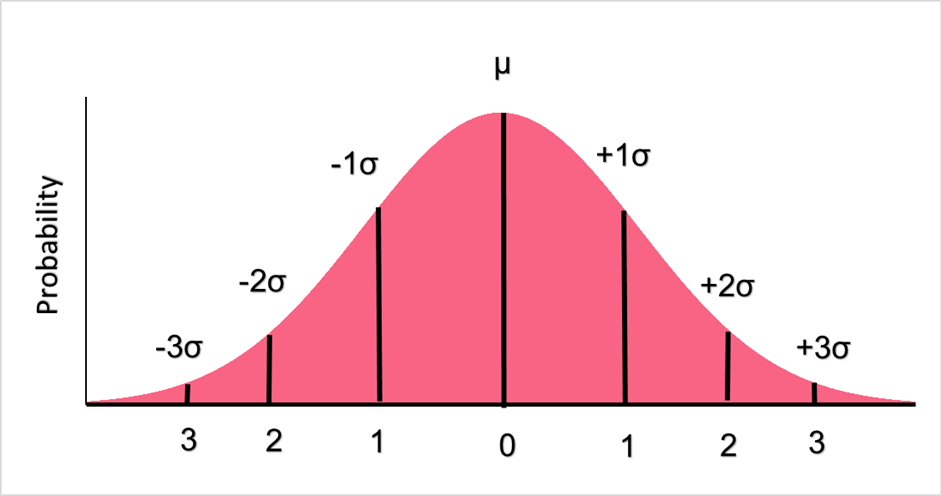
A standard normal distribution has a mean equal to zero and a standard deviation equal to sigma,  . This doesn’t mean that the mean is actually zero, but that the z-score of the mean is zero. The z-score is simply the standardised version of a given number, whose formula can be found below.
. This doesn’t mean that the mean is actually zero, but that the z-score of the mean is zero. The z-score is simply the standardised version of a given number, whose formula can be found below.

You want to know the probability that an individual will score below 40 points on the upcoming exam if the mean for the exam is 60 and the standard deviation is 6.5.
Standard Normal Distribution Solution
In order to solve this problem, we will first plot our information on the standard normal distribution.
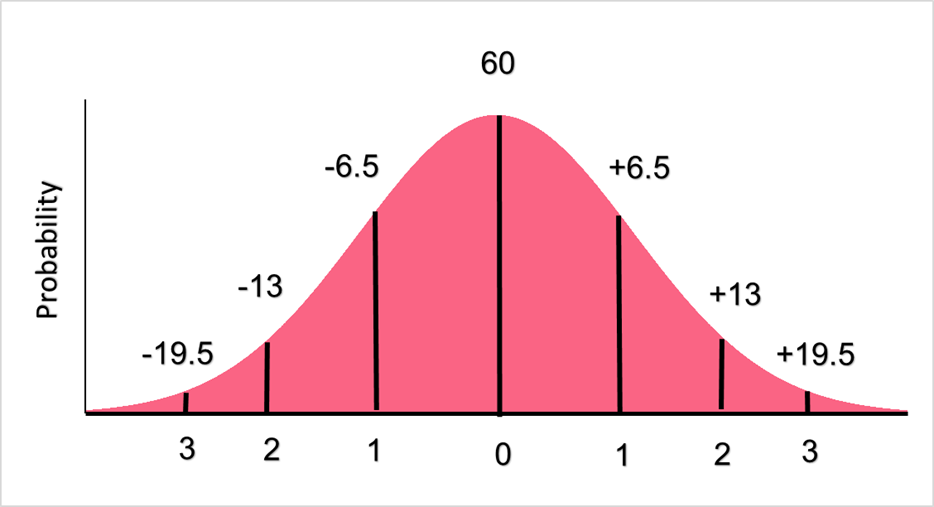
To understand the image above, go back to our description of what a standard normal distribution is. The mean has a standard score of zero, the reason for which can be seen below.

Zero divided by any number is equal to zero, which means that the average of the data will always have a z-score of zero. One standard deviation below the mean score is 33.5 points while one standard deviation above the mean is 46.5 points.
We are interested in determining the probability of scoring below 40 points. This means we are interested in a one-tail test, which is simply another way of saying we’re only interested in one side of the distribution. First, we find the z-score of 40 and then find this z-score on the z-table, which lists all the probabilities of each z-score.
\[
z-score = \frac{40-60}{6.5} = -3.077
\]
Looking at this on a z-table, which are widely available online, we get 0.0011. This means that the probability of scoring less than 40 points on the exam is less than about 0.1%. In other words, highly unlikely.
Poisson Distribution Problem
Poisson distributions are distinct from standard normal distributions. While it is still a probability distribution, it is a distribution that deals with the number of “successes” in a time interval. Success here is anything we want to measure - for example, the number of times someone calls a support hotline. The mean of a Poisson distribution is depicted by lambda, 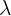 . The probability of a poison distribution is calculated by the following formula.
. The probability of a poison distribution is calculated by the following formula.
\[
P(x) = \frac{\lambda^{x} e^{\lambda}}{x!}
\]
Where lambda is the mean successes in a given time interval and x is the number we want to test. The e in the equation is the natural log, which can be found on most calculators and is equal to about 2.72. The x! in the denominator is a factorial, which is a function also found on most calculators.
For example, say that the mean number of customers calling a hotline in an hour is 5 and we’re interested in knowing the probability that 10 people will call in an hour. Our lambda here would be 5 and our x would be 10, which we would simply plug into the equation.
Poisson Distribution Solution
Let’s continue from the previous example and say that you’re interested in knowing two different probabilities.
- The probability that 8 people will call in one hour
- The probability that 18 people will call in three hours
Recall that our 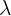 here is 5. For the first problem, we simply plug 8 into the equation.
here is 5. For the first problem, we simply plug 8 into the equation.
\[
P(X=8) = \frac{5^{8} e^{-5}}{8!} = 0.06528
\]
The first probability, as we can see from the result, is about 6.5%. In other words, it is pretty unlikely that 10 people will call the hotline in one hour.
The second question is a bit more tricky. You may be wondering what to do in situations where the time interval being asked for exceeds the time interval we have information on. Here, we simply multiply the mean by the number of time intervals we have. This is illustrated below.
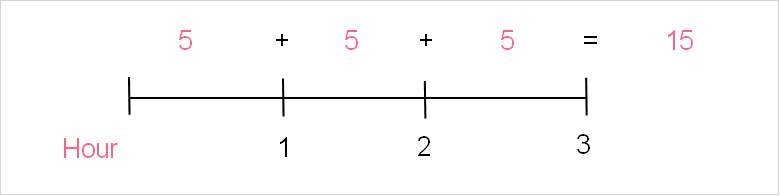
Since our lambda deals with a one-hour interval, we can see that there are 3 one-hour intervals here. Therefore, we simply multiply 5 times 3 to get a lambda of 15. Next, we plug this into the equation.
\[
P(X=18) = \frac{15^{18} e^{-15}}{18!} = 0.07061
\]
Therefore, the probability of getting 18 calls within 3 hours is about 7%.













