
Introduction
We use averages every day—whether it's calculating a batting average in cricket, the average temperature for the month, or the average score on a test. In statistics, this concept is formally known as the arithmetic mean.
The arithmetic mean (often just called the "mean") is the sum of all values divided by the total number of observations. While simple to calculate for small lists of numbers, it requires different techniques when dealing with large datasets or grouped data (intervals).
In this article, we will practice finding the mean using raw data, frequency tables, and grouped distributions.
Practice Questions & Solutions
Find the mean for the following set of numbers: 3, 5, 2, 6, 5, 9, 5, 2, 8, 6
Step 1: Find the sum of the values: 3 + 5 + 2 + 6 + 5 + 9 + 5 + 2 + 8 + 6 = 51
Step 2: Count the number of values - there are n = 10 numbers.
Step 3: Apply the formula
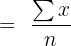
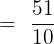
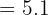
Calculate the mean for the following large set of numbers: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4
When data repeats frequently, it is faster to group the numbers by how often they appear (frequency).
Step 1: Group the data (Value: Frequency)
2: appears 2 times
3: appears 2 times
4: appears 5 times
5: appears 6 times
6: appears 2 times
8: appears 3 times
Step 2: Calculate the product (x * f) - multiply each value by its frequency:
2 * 2 = 4
3 * 2 = 6
4 * 5 = 20
5 * 6 = 30
6 * 2 = 12
8 * 3 = 24
Step 3: Take the sum = 96
Step 4: Apply the weighted mean formula
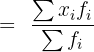
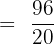
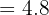
Calculate the mean for the statistical distribution given below:
Value (x): 61, Frequency (f): 5
Value (x): 64, Frequency (f): 18
Value (x): 67, Frequency (f): 42
Value (x): 70, Frequency (f): 27
Value (x): 73, Frequency (f): 8
This is a standard weighted mean problem. We need to find the total sum of all values by multiplying each score (x) by its frequency (f).
Step 1: Calculate x * f for each pair
61 * 5 = 305
64 * 18 = 1152
67 * 42 = 2814
70 * 27 = 1890
73 * 8 = 584
Step 2: Sum the total frequency = 5 + 18 + 42 + 27 + 8 = 100 and the total value = 305 + 1152 + 2814 + 1890 + 584 = 6745
Step 3: Calculate the mean
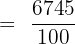
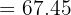
A statistical distribution is given by the following intervals (grouped data). Calculate the mean.
[10, 15): Frequency 3
[15, 20): Frequency 5
[20, 25): Frequency 7
[25, 30): Frequency 4
[30, 35): Frequency 2
When data is grouped into intervals (classes), we cannot use the exact values. Instead, we use the class mark (midpoint) of each interval to represent x.
Step 1: Find the Class Mark (x) for each interval Formula: (Lower Limit + Upper Limit) / 2
[10, 15): (10+15)/2 = 12.5
[15, 20): (15+20)/2 = 17.5
[20, 25): (20+25)/2 = 22.5
[25, 30): (25+30)/2 = 27.5
[30, 35): (30+35)/2 = 32.5
Step 2: Multiply frequency by class mark (x * f)
12.5 * 3 = 37.5
17.5 * 5 = 87.5
22.5 * 7 = 157.5
27.5 * 4 = 110.0
32.5 * 2 = 65.0
Step 3: Calculate sum of frequencies = 3 + 5 + 7 + 4 + 2 = 21 and sum of products = 457.5
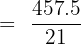
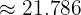
Given the statistical distribution below, calculate the mean:
[0, 5): Frequency 3
[5, 10): Frequency 5
[10, 15): Frequency 7
[15, 20): Frequency 8
[20, 25): Frequency 2
[25, ∞): Frequency 6
To calculate the mean of grouped data, we require a defined class mark (midpoint) for every interval.
Look closely at the final interval: [25, ∞). This is an open-ended interval. Because the upper limit is infinity, we cannot calculate a midpoint (x).
The mean cannot be calculated for this distribution because the class mark of the last interval is undefined. We would need more specific data about the values in that final group to proceed.
Summarise with AI:












