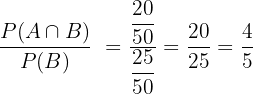In this article, we will solve some examples related to probability. So, let us get started.

Example 1
In a class of 32 students, 25 take mathematics, 22 take science, and 15 students take both mathematics and science. Find the probability that a randomly selected student:
a) takes mathematics only
b) takes science only
c) takes mathematics
d) takes science
e) takes mathematics and science
f) takes mathematics given that he already takes science
Solution
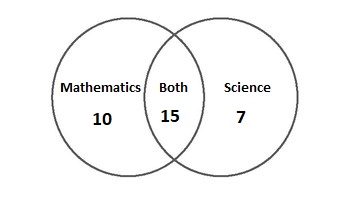
This question has many parts. We will solve each part one by one, but first, we will draw a Venn diagram from the information in the question like this:
Part a
Number of students who take mathematics only = 10
Total number of students in the class = 32
Probability that a randomly selected student takes mathematics only = P(A) = 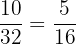
Part b
Number of students who take science only = 7
Total number of students in the class = 32
Probability that a randomly selected student takes science only = P(B) = 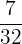
Part c
Number of students who take mathematics = 10 + 15 = 25
Total number of students in the class = 32
Probability that a randomly selected student takes mathematics = P(C) = 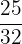
Part d
Number of students who take science = 7 + 15 = 22
Total number of students in the class = 32
Probability that a randomly selected student takes science = P(D) = 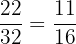
Part e
Number of students who take both mathematics and science = 15
Total number of students in the class = 32
The probability that randomly selected student takes both mathematics and science = 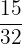
Part f
Number of students who take science = 7 + 15 = 22
Number of students who take mathematics and science = 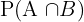 = 15
= 15
Probability that a randomly selected student takes mathematics, given that he already takes science = 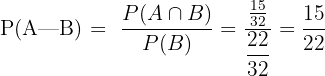
Example 2
Two friends go hunting. The first friend kills an average of 3 animals every 6 shots and the friend kills two animals every 7 shots. If the two fired at the same animal at the same time, find the probability that they will obtain a kill.
Solution
Suppose A be an event that the first friend obtains a kill. Then the probability of obtaining a kill of the first friend will be represented by P(A).
Probability of the first friend obtaining a kill = P(A) = 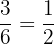
Suppose B be an event that the second friend obtains a kill. Then the probability of obtaining a kill of the second friend will be represented by P(B).
Probability of the second friend obtaining a kill = P(B) = 
The probability of first and second friend obtaining a kill = 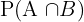 =
= 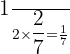
Probability that both the friends obtain a kill = 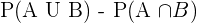 =
= 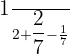
= 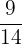
Example 3
The probability that the annual event will be held on a specific day is 0.57. Find the probability that:
a) the event will not be held on that day
b) the event will take place or not take place on that day
Solution
Part a
The probability of event taking place at a certain day = P(E) = 0.57
The probability of event not taking place at a certain day = P(E)' = 1 - P(E) = 1 - 0.57 = 0.43
Part b
Probability of event taking place at a certain day = P(E) = 0.57
Probability of event not taking place at a certain day = P(E)' = 1 - P(E) = 1 - 0.57 = 0.43
The probability of event taking place or not taking place on a certain day = P(E U E') = 0.57 + 0.43 = 1.00
Example 4
Solution
Total number of groups = 3
The number of groups from which a student who likes mathematics will be selected = 1
Probability = P (B_i) = 
Total number of students in the first group = 20
Number of students who like mathematics = 5
Probability of choosing a student who likes mathematics from the first group = 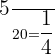
Total number of students in the second group = 12
Number of students in the second group who like mathematics = 7
Probability of choosing a student who likes mathematics from the second group = 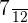
Total number of students in the third group = 18
Number of students who like mathematics in the third group = 3
Probability of choosing a student who like mathematics from the third group = 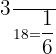
The probability of choosing the student who likes mathematics from one of the three groups will be calculated using the total probability rule.
P (girl) = 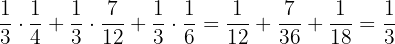
Example 5
In a group of 50 people, 35 own a car, 25 own a bike, and 20 own both a car and a bike. 10 people neither own a car nor a bike. Find the probability that a randomly selected person:
a) owns a car only
b) owns a bike only
c) owns a car
d) owns a bike
e) owns a car and a bike
f) neither owns a car nor a bike
g) owns a car given that he already has a bike
Solution
This question has many parts. We will solve each part one by one, but first, we will draw a Venn diagram from the information in the question like this:
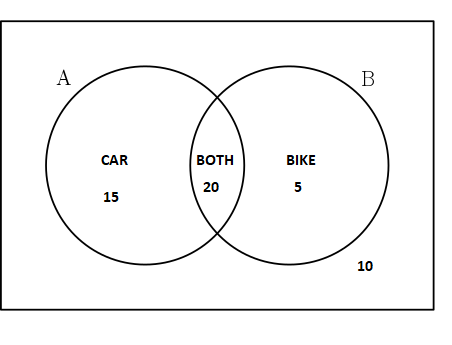
Part a
Number of people who have a car only = 15
Total number of people = 50
Probability that a randomly selected person owns a car only = P(A) = 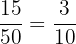
Part b
Number of people who have bike only = 5
Total number of people = 50
Probability that a randomly selected person owns a bike only = P(B) = 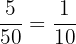
Part c
Number of people who own a car = 20 + 15 = 35
Total number of people = 50
Probability that a randomly selected person owns a car = P(C) = 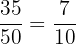
Part d
Number of people who own bike = 5 + 20 = 25
Total number of people = 50
Probability that a randomly selected person owns a bike = P(D) = 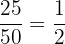
Part e
Number of students who take own a car and a bike both = 20
Total number of people = 50
The probability that a randomly selected person owns a car and a bike = 
Part f
Number of people who neither own a car nor a bike = 10
Total number of people = 50
The probability that a randomly selected person neither owns a car nor a bike = 
Part g
Probability that a randomly selected person owns a car given that he already has a bike = P(A|B) =