In this article, you will learn what is conditional probability and how to solve the questions related to this concept. So, let us get started.

Conditional Probability
There are two types of events that occur randomly in our lives:
a) Independent events
These events are not affected by other events. For example, rolling the dice on the floor. This event is not influenced by any other event; therefore it is termed as an independent event. In mathematics, we have notations for everything. We denote the simple probability as:
P(A)
b) Dependent events
These events are dependent on other events, i.e. they are affected by other events.
Suppose that you choose a ball from a set of 8 colored balls and do not replace it. Next time, you choose another ball from the set. The second time the probability changes because, in the beginning, the total number of balls was 8, but the next time, 7 balls were left. Therefore, the second event is dependent on the first one. However, if there is a condition that the ball is replaced each time it is picked, then the events will be independent.
A conditional probability is finding the probability of an event that is dependent on another event.
The mathematical notation of conditional probability is:
P(A|B)
It is read as the probability of event A given event B. The formula for finding the conditional probability of two events A and B is given below:

We can also swap the sides of this formula according to the question like this:

Now, we will solve some examples of conditional probability to understand the concept better.
Example 1
What is the probability of selecting two queen cards from the deck of 52 cards?
Solution
To solve the problems related to the cards in a deck, you should know which types of cards are present in each deck. The properties of a deck are given below:
- There are four suits in a deck
- Two suits have black cards and two of them are red
- In each suit, there are 13 cards. These 13 cards include a queen, a king a jack, ace, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
In a deck of 52 cards, there are 4 queen cards. Since we need to select the two cards from the deck, hence, first, we will find the probability of selecting the first card from the deck.
Number of queen cards in a deck = 4
Total number of cards in a deck = 52
The probability of selecting a queen card from a deck = 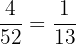
Now, we will compute the probability of picking up the second card from the deck.
Number of queen cards left in a deck = 3
Total number of cards left in a deck = 51
The probability of picking up a queen card, given that a queen card has already been selected = 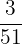
In this example, we need to tell the probability of picking up two queen cards, therefore we will multiply the probabilities above:
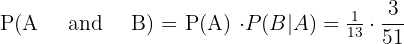
= 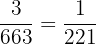
Example 2
What is the probability of selecting two black cards from the deck of 52 cards?
Solution
Refer to the types of cards that are present in a deck. Out of 52 cards in a deck, two suits have black cards and two of them are red. A deck is divided into 4 suits and each suit has 13 cards.
In a deck of 52 cards, there are 26 black cards. Since we need to select the two cards from the deck, hence, first, we will find the probability of selecting the first card from the deck.
Number of black cards in a deck = 26
Total number of cards in a deck = 52
The probability of selecting a black card from a deck = 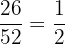
Now, we will compute the probability of picking up the second card from the deck.
Number of black cards left in a deck = 25
Total number of cards left in a deck = 51
The probability of picking up a black card, given that one black card has already been selected = 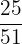
In this example, we have to tell the probability that both cards selected are black. Hence, we will multiply the probabilities like this:
= 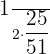
= 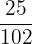
Example 3
There are 12 balls in the pool. 6 balls are blue and the rest are red. Two of the balls are picked up from the pool without replacement. What is the probability of selecting two red balls from the pool?
Solution
We will calculate the probability of the first ball.
Total number of balls in the pool = 12
Probability that a randomly selected ball is red = 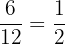
Now, we will compute the probability of the second ball.
Total number of balls left in the pool = 11
Number of red balls left in the pool = 5
Probability of selecting a red ball second time = 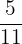
Probability that two balls selected randomly are red in color = P(A) x P(B|A) = 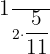
= 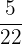
Example 4
There are 8 blue, 7 green, and 6 red-colored pens in a packet. Suppose you draw 2 pens at random from the packet and do not replace them. You then draw another pen. What is the probability that two pens drawn are green and one is red?
Solution
First, we will find the probability of drawing one green pen from the packet.
Number of green pens in the packet = 7
Total number of pens in the packet = 21
The probability of drawing one green pen from the packet = 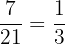
Now, we will compute the probability of drawing a green pen the second time.
Number of green pens left in the packet = 6
Total number of pens left in the packet = 20
The probability of picking up a green pen second time = 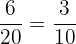
We have to select three pens. Hence, we will also compute the probability of picking up a red pen from the packet after two green pens were selected.
Number of red pens in the packet = 6
Total number of pens in the packet left = 19
The probability of picking up a third pen that is red = 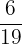
Probability of picking up two green and one red pen = 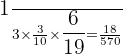
Example 5
In a class, 35% of the students study science and history. 65% of the students study science. What is the probability of a student studying history given he/she is already studying science?
Solution
Percentage of the students studying science and history = 35%
Probability of students studying science and history = P(S and H) = 0.35
Percentage of students studying science = 65%
The probability of students studying science = P(S) = 0.65
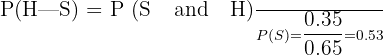













Iam unable to understand
I specified that I wanted 7th-grader stuff but these are not even in my whole textbook
Someone relook at the examples. What z table are you referring to? Once you solve for the Z the rest of the answer is gibberish. Maybe sh o w the table, label the axes and red line the values you call out so the student can figure out what you are trying to convey.
Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian
I’m a junior high school,500 students were randomly selected.240 liked ice cream,200 liked milk tea and 180 liked both ice cream and milktea
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
Where is the answer??
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?