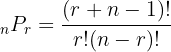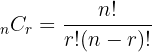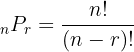Chapters

Combinatorics Definition
| Definition | Notation | |
| Combination | A combination of numbers where the order of them doesn’t matter | 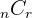 |
| Permutation | A combination of numbers where the order of them does matter | 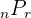 |
The table above shows the main difference between a combination and a permutation. Keep in mind that n is the number of things we pick from while r is how many we pick from them. Within each style of counting, you have two different types of groups of numbers:
- With repetition
- Without repetition
Combinations and Permutations
In order to understand how to calculate combinations and permutations, let’s look at the formulas and some examples of each.
| Combination | Permutation | |
| With repetition | Ice cream flavours
| Code for a phone password
|
| Without repetition | Lottery numbers
| Order of the first 4 people who finish their test
|
Permutations with Repetition
We want to guess the 5-digit code for a phone with numbers 0-9, which is:
- A permutation, because the order you input matters
- With repetition, because you can pick the same numbers more than once
Here, we have 10 numbers to choose from (n) and 5 we can choose from (r).
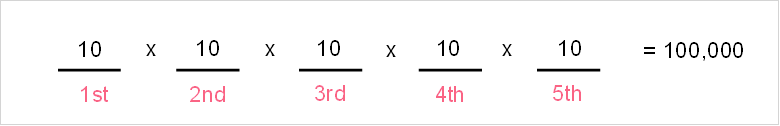
To understand the formula, think about if we could only choose 2 numbers out of 4 or 5.
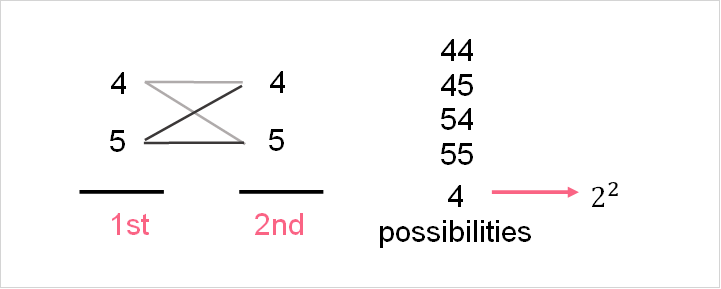
Because the order matters, the combinations 4,5 and 5,4 are completely different.
Permutations without Repetition
The first 4 people of a class of 15 that finish their exam is:
- A permutation, because order matters
- Without repetition, because someone can’t finish 2nd and 4th at the same time
Here, we have 15 students (n) and we choose only 4 (r).
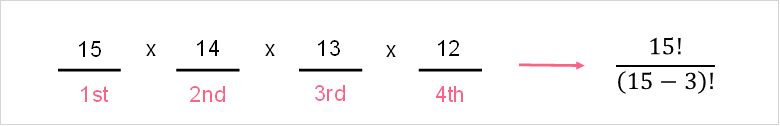
Because there’s no repetition, the number of students we can choose from reduces each time.
Combinations with Repetition
Choosing 2 ice cream flavours out of 3 is:
- A combination, because the order you choose the flavours doesn’t matter
- With repetition, because you can choose the same flavour more than once
Here, we have 3 flavours to choose from (n) and 2 we can choose (r).

Because order doesn’t matter, choosing flavours 1,2 is the same as choosing flavours 2,1.
Combinations without Repetition
We choose 2 lottery numbers out of 4 numbers: 0,1,2,3. This is:
- A combination because order doesn’t matter
- Without repetition because we can only chose each number once
We have 4 numbers to choose from (n), where we can choose 2 (r).
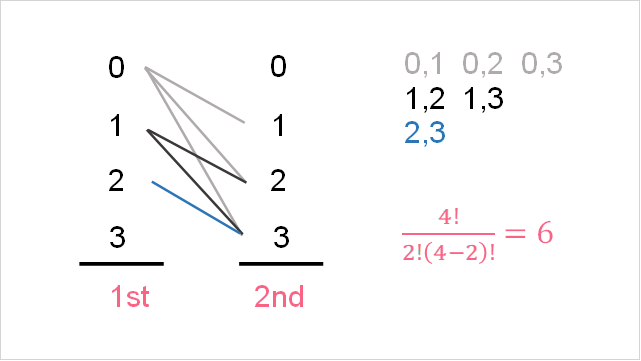
Because order doesn’t matter, the combination 0,1 would be the same as 1,0. Because we can’t have repetition, we can’t use: (0,0), (1,1), (2,2) or (3,3).
Sample Space
Within probability, there is a concept known as a random variable. A random variable is different from the traditional variables you’re used to seeing in algebra. You can think of a random variable as a variable whose outcome is unknown until the moment it happens.

The image above shows some common examples of random variables you’ll see in statistics. A sample space is all the possible outcomes that a random variable can take on. The sample spaces of a coin toss and a die roll are illustrated below.

When we talk about the probability of something, or the likelihood of something happening, we typically talk about the probability of an event occurring. An event is one or more outcomes from the sample space. Take a look at some events below.

Probability
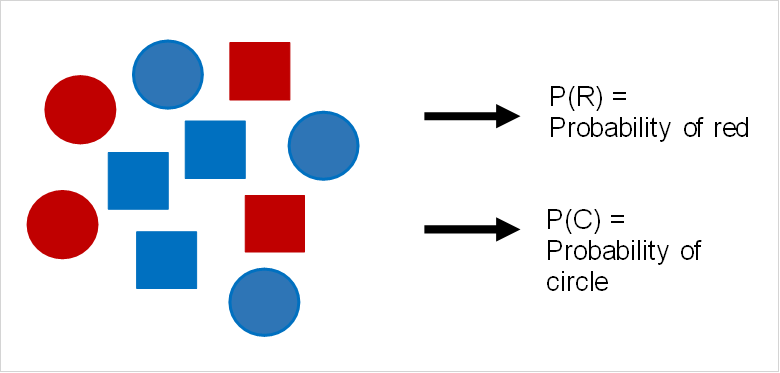
Probability is the likelihood that an event will occur. The simplest equation for probability is simply the number of ways or times an event can occur over the total sample space. Take the following as an example.

If we wanted to find the probability of picking a red square, we would simply divide the number of red squares, 2, over all possibilities, 10. Take a look at some more events and probabilities below.
| Event | Probability | P in % |
| Picking a blue shape | 6/10 | 60% |
| Picking a red shape | 4/10 | 40% |
| Picking a square | 5/10 | 50% |
| Picking a circle | 5/10 | 50% |
Independent Event
An independent event is an event whose probability is not affected by the outcome of another event. The most basic example of this is selection with replacement, which simply means you put back the item you’ve selected.

| Description | Probability | |
| Step 1 | You have a deck of 5 cards: 1 king, 2 queens and 2 aces. What is the probability of selecting an ace? | 2/5 |
| Step 2 | You pick a card and you have selected a king. You put this card back in the deck. What is the probability of selecting an ace? | 2/5 |
In the table above, you can see two events, which happen right after one another. The probability of each is the same.
Dependent Event
A dependent event is an event whose probability is dependent on the outcome of another event. A common example of this is probability without replacement. Take the example from the previous section.
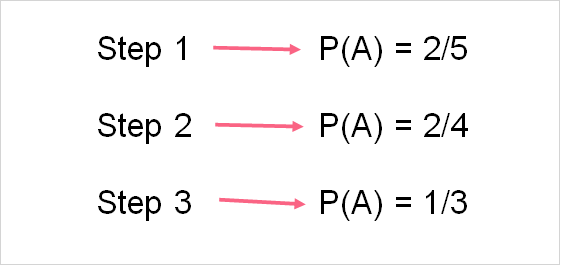
| Description | Probability | |
| Step 1 | You have a deck of 5 cards: 1 king, 2 queens and 2 aces. What is the probability of selecting an ace? | 2/5 |
| Step 2 | You pick a card and you have selected a king. You do not put this card back in the deck. What is the probability of selecting an ace? | 2/4 |
| Step 3 | You pick another card and it’s an ace. You don’t put this card back. What is the probability of selecting an ace? | 1/3 |
As you can see, the probability of the event depends on what happened in the event before it.
Conditional Probability
Conditional probability is the probability of two dependent events that are not mutually exclusive. Mutually exclusive events are events that can’t occur at the same time. Let’s go back to our earlier example.
From the image, you can see there are two events.
| Probability | Description | |
| Mutually Exclusive | P(R and S) = 2/10 | You can pick a red shape and a square shape at the same time, as there are 2 red squares |
| Not Mutually Exclusive | P(C and S) = 0 | You cannot pick a circle and a square shape at the same time, it’s impossible |
Bayes’ Theorem
Bayes’ theorem is a very helpful equation that we can use when we already know the conditional probability of two events.
\[
P(A|B) = \frac{P(A) P(B|A)}{P(B)}
\]
| P(A|B) | Conditional probability of A on B, meaning the probability of A given B has occurred |
| P(A) | Probability of event A |
| P(B|A) | Conditional probability of B on A, meaning the probability of B given A has occurred |
| P(B) | Probability of event B |
Bayes’ Theorem Example
Take the following example for the Bayes' theorem:
| Example | Description | |
| P(A|B) | ? | Probability of an infectious disease given a fever |
| P(A) | 0.6 | Probability of infectious disease |
| P(B|A) | 0.1 | Probability of fever given infectious disease |
| P(B) | 0.4 | Probability of fever |
To find the conditional probability, we simply plug these into the equation.
| Equation | Value | |
| P(A) * P(B|A) | 0.6 * 0.1 | 0.06 |
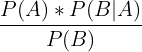 | 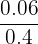 | 0.15 |