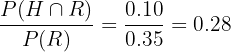In this article, you will find detailed answers to the probability questions. So, let us get started.

Example 1
Sam wants to go to the doctor for a regular checkup. The probabilities of visiting a doctor with or without traffic are 0.33 and 0.74 respectively. If the probability of traffic on a certain day is 0.53, then determine the probability that John will go to the doctor?
Solution
Suppose A be the event that John will go to the doctor and B be the event that there is traffic. We have the following information:
P(B) = 0.53
P(no traffic) = P(B′) = 1 − P(B) = 1 − 0.53 = 0.47
The conditional probabilities of these events will be:
P(A|B) = 0.33
P(A|B') = 0.74
We know that the events B and B' form the partitions of the sample space, S, so, using the total probability theorem, we will compute the probability like this:
P(A) = P(B) P(A|B) + P(B′) P(A|B′)
= 0.53 x 0.33 + 0.47 x 0.74
= 0.5227
Example 2
Suppose three dice are rolled simultaneously. What is the probability of getting a multiple of 2 on the first die, a composite number on the second die, and 3 or 5 on the third die?
Solution
Total number of possible outcomes on a single die = 6
Probability of getting a multiple of 2 on the first die = 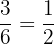
Probability of getting a composite number on the second die = 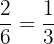
Probability of getting 3 or 5 on the third die = 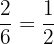
The probability of getting a multiple of 2 on the first die, a composite number on the second die, and 3 or 5 on the third die = 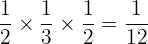
Example 4
In a class, 25% of the students play badminton, 40% play tennis, and 10% play both tennis and badminton. Suppose a student is chosen at random. If he/she plays tennis, what is the probability that he/she has also plays badminton?
Solution
Probability of the student playing a tennis = P(T) = 0.40
Probability of playing both badminton and tennis = 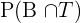 = 0.10
= 0.10
P (Badminton|Tennis) = 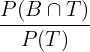
= 
Example 5
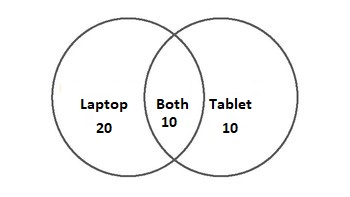
In a class of 40 students, 30 have a laptop, 20 have a tablet, and 10 students have a laptop and tablet both. Find the probability that a randomly selected student:
a) have a laptop only
b) have a tablet only
c) have a laptop
d) have tablet
e) have tablet and laptop
f) have laptop given that he/she already owns a tablet
g) have a tablet given that he/she already owns a laptop
Solution
This example has several parts, so we will solve each part one by one. But before proceeding to solve the parts, first, we will draw a Venn diagram using the information from the examples like this:
Part a
Total number of students in a class = 40
Number of students who own a laptop only = 20
Probability of randomly selected student owning a laptop only = 
Part b
Total number of students in a class = 40
Number of students who own a tablet only = 10
Probability of randomly selected student owning a tablet only = 
Part c
Total number of students in a class = 40
Number of students who own a laptop = 30
Probability of randomly selected student owning a laptop = 
Part d
Total number of students in a class = 40
Number of students who own a tablet = 20
Probability of randomly selected student owning a tablet = 
Part e
Total number of students in a class = 40
Number of students who own a laptop and a tablet = 10
Probability of randomly selected student owning a laptop and a tablet = 
Part f
Probability of randomly selected student owning a laptop and a tablet = 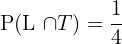
Probability of randomly selected student owning a tablet = 
Probability of randomly selected student having laptop given that he/she already own a tablet = P(L|T) = 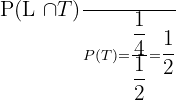
Part g
Probability of randomly selected student owning a laptop and a tablet = 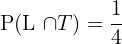
Probability of randomly selected student owning a laptop = 
Probability of randomly selected student having a tablet given that he/she already owns a laptop = P(T|L) = 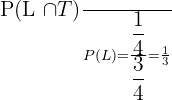
Example 6
In a box, there are 15 almonds, 18 cashew nuts, 25 peanuts, and 12 pistachios. What is the probability of:
a) drawing an almond randomly
b) drawing two cashew nuts
c) drawing a pistachio and then an almond without replacement
d) drawing an almond and then a peanut without replacement
e) drawing a dry fruit that is not pistachio
f) drawing an almond or a pistachio
Solution
Part a
Total number of dry fruits in a box = 15 + 18 + 12 + 25 = 70
Number of almonds in a box = 15
Probability of drawing an almond = 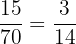
Part b
Total number of dry fruits in a box = 70
Number of cashew nuts = 18
Probability of drawing a single cashew nut = 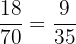
Probability of drawing a cashew nut again = 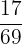
The probability of drawing two cashew nuts = 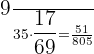
Part c
Total number of dry fruits in a box = 70
Number of pistachios in a box = 12
The probability of drawing a pistachio from the box = 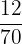
Number of almonds in a box = 15
Probability of drawing an almond from the box = 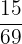
Probability of drawing pistachio and then an almond from a box = 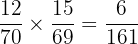
Part d
Total number of dry fruits in a box = 70
Number of almonds in a box = 15
Probability of drawing an almond from the box = 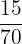
Number of peanuts in a box = 25
Probability of drawing a peanut from the box after almond = 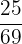
The probability of drawing an almond and then a peanut from the box = 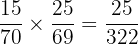
Part e
Total number of dry fruits in a box = 70
Number of pistachio in the box = 12
Number of dry fruits which aren't pistachios = 70 - 12 = 58
The probability of drawing a dry fruit which isn't a pistachio = 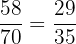
Part f
Total number of dry fruits in a box = 70
Number of almonds in the box = 15
Number of pistachios in the box = 12
Probability of drawing an almond or a pistachio from the box = 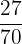
Example 7
50% of the residents in a certain area own a house. 35% of the residents live on rent, while 10% own a house and live on rent. For a randomly selected person, calculate the probability that the person owns a home, given that he lives on rent.
Solution
Probability of randomly selected person owning a house = 0.50
Probability of randomly selected person living on rent = 0.35
Probability of randomly selected person owning a house and living on rent = 0.10
The probability of randomly selected student owning a house, given that he is living on rent = P(H|R) =