Chapters

What is Frequency?
When people think about modern statistics, they often think about the immense advancements in the realm of machine learning and artificial intelligence. While self-driving cars and robots are incredible uses of science and maths, the majority of the statistics that are used on a daily basis are really quite simple. Frequency, a descriptive statistic, is one example of this.
Frequency is defined as the number of times something occurs. Take a look at some examples below.
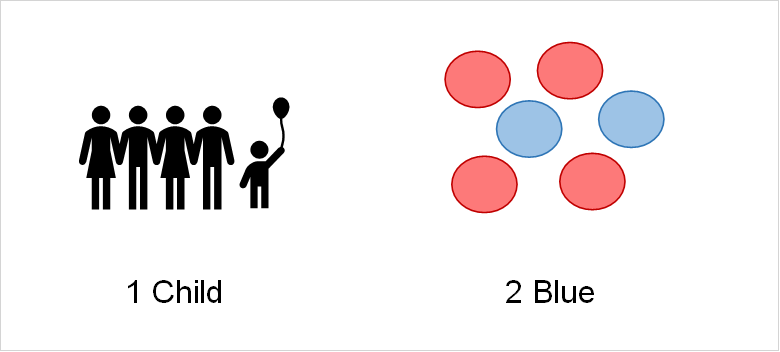
As you can see above, the frequency is calculated by simply counting the number of times something occurs. The information displayed in the chart above would normally be summarised as in the table below.
| Frequency | Frequency | |
| People | 1 child | 3 adults |
| Marbles | 2 blue | 4 red |
Frequency Distribution
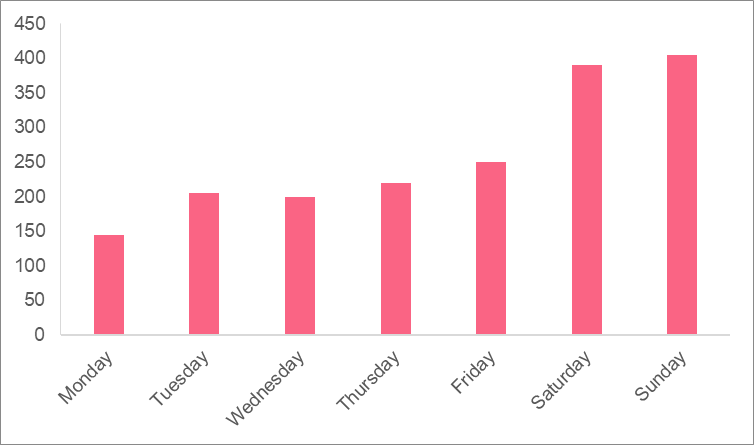
While a frequency distribution can be a formula, a frequency distribution is most often a visual representation of the frequency. Regardless of how its displayed, a frequency distribution helps us get a better understanding of how a variable is distributed, or how a variable looks like. The following table gives the number of passengers riding the bus for every day of the week.
| Day | Frequency |
| Monday | 145 |
| Tuesday | 205 |
| Wednesday | 199 |
| Thursday | 220 |
| Friday | 250 |
| Saturday | 390 |
| Sunday | 405 |
While having this information in a table is very handy, it can often be difficult to understand in plain numbers. Showing the frequency distribution is an easy way to present the frequency in a more understandable manner.
What is Probability?
In order to define probability, there are a couple of basic definitions you must understand first. These definitions, along with examples, are listed below.
| Concept | Definition | Example | Notation |
| Random Variable | A variable whose outcome is unknown | The outcome of a toss of a coin | Usually a capital letter like  |
| Sample Space | All possible outcomes of a random variable | Heads and tails | S = {H,T} |
| Event | One or more outcomes in a sample space | Heads | A = H |
Probability is defined as the chance, or likelihood, of an event occurring. Continuing the table above:
| Concept | Definition | Example | Notation |
| Probability | The chance of an event occurring | The probability of landing on heads (event A) | P(A) = 0.5 (50%) |
Probability Distribution
A probability distribution is a visualization that allows you to see all possible values a random variable can take on along with the probability of each value occurring. While this can sound like a strange concept, we can think about it in terms of the heights of people in the population.
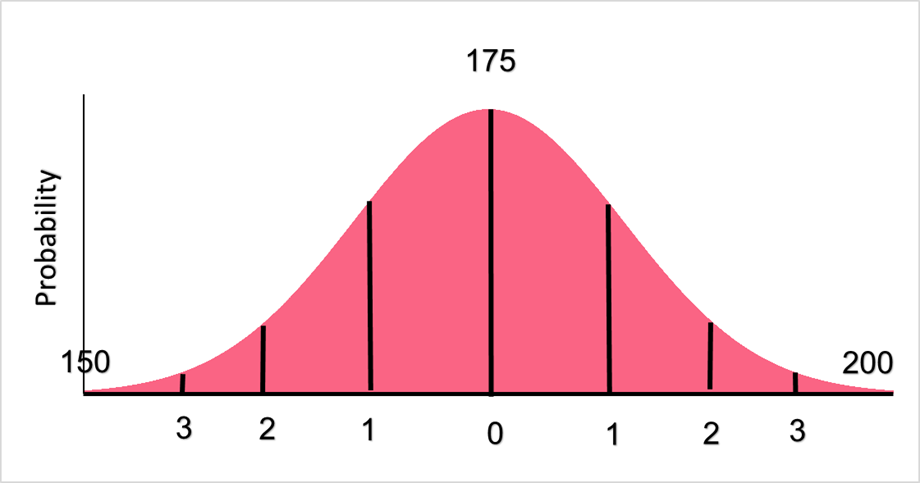
The image above is an example of a probability distribution for heights, where the average height is 175 cm. The distribution shows us that heights that are on the lower and upper end, such as 150 or 200 cm, are much less common in the population. In other words, it is less probable that someone’s height be at either of these ends.
Types of Distributions
As you can guess, different variables have different distributions. Knowing the distribution of a variable allows us to be able to calculate probabilities. This is because each distribution has a probability equation.
| Distribution | Parameters | Equation |
| Standard Normal | N( , , 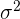 ) ) | 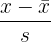 |
| Binomial | B(n,p) | 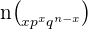 |
| Poisson | Po(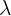 ) ) | 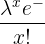 |
The table above shows the three most common probability distributions. The standard normal distribution is quite special. One major difference is that it’s probability can only be found along with a z-table.
Normal Distribution
A normal distribution is a continuous probability distribution that is symmetric and has a bell shape. A standard normal distribution is similar to a normal one. Instead of having the variable of interest on the x-axis as a raw score, or a plain number, a standard normal distribution shows each value of the random variable in terms of the standard deviation. Each value is standardized using the equation in the table above, resulting in what is known as a z-score.
| Z | 0 | 0.01 | 0.02 | 0.03 | 0.04 |
| 0 | 0.50000 | 0.50399 | 0.50798 | 0.51197 | 0.51595 |
| 0.1 | 0.53983 | 0.54380 | 0.54776 | 0.55172 | 0.55567 |
| 0.2 | 0.57926 | 0.58317 | 0.58706 | 0.59095 | 0.59483 |
| 0.3 | 0.61791 | 0.62172 | 0.62552 | 0.62930 | 0.63307 |
The table above shows an example of a z-table. The image below shows how to look up a z-score on a z-table.
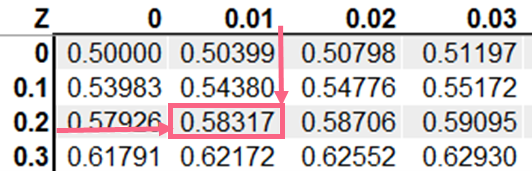
Problem 1
We are interested in knowing how likely it is for one type of tree to grow to a certain length. The length of these trees exhibit a normal distribution. The tree that you measure is 120 cm. Given the following information, do you think this tree length is uncommon for this type of tree?
- Mean: 100
- Standard deviation: 10
- Formula:
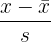
Solution 1
In order to solve this problem, we first need to understand what this distribution will look like. Remember that a standard normal distribution has the mean at the center, with a z-score of 0. The image below represents the mean and the distribution of the tree heights.
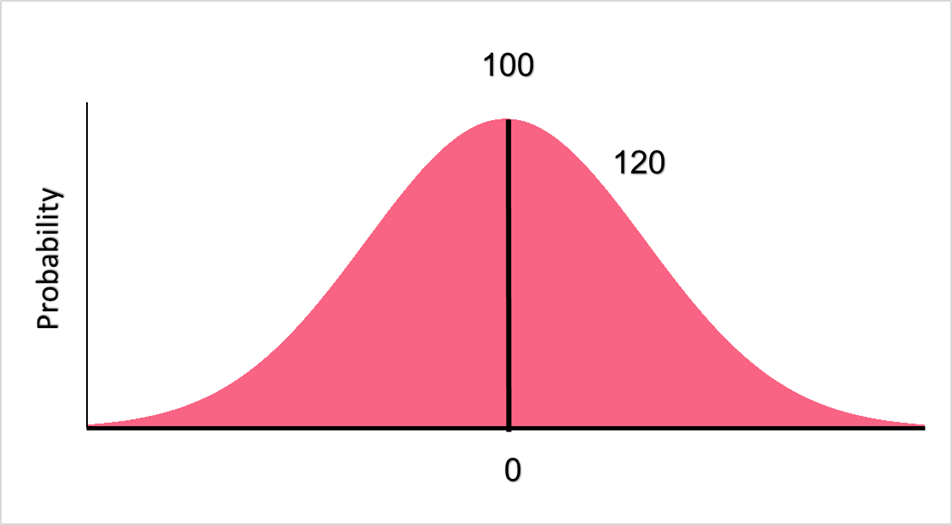
For now, we know that 120cm is located to the right of 100 on the distribution. In order to find its exact location, we need to find the z-score of 120.
\[
z-score = \frac{120-100}{10} = 2
\]
The z-score is 2, which means that the height of 120 is 2 standard deviations above the mean height of 100. Next, we can find this z-score on a z-table.
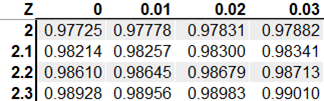
This gives us a probability 0.9772, which is very likely.
Problem 2
You are interested in how uniform the lengths of socks are that are produced at a factory. You measure the distribution and see that there is a normal distribution for the length of the socks. Given the following information, how likely is it that a sock is above 25 cm.
- Mean: 20
- Standard deviation: 10.5
- Formula:
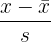
Solution 2
This time, we want to know how likely it is for a sock to have a length at and above 25 cm. This means that we are looking for a right tail probability instead of a left tail probability. Looking at the distribution will help you understand why.
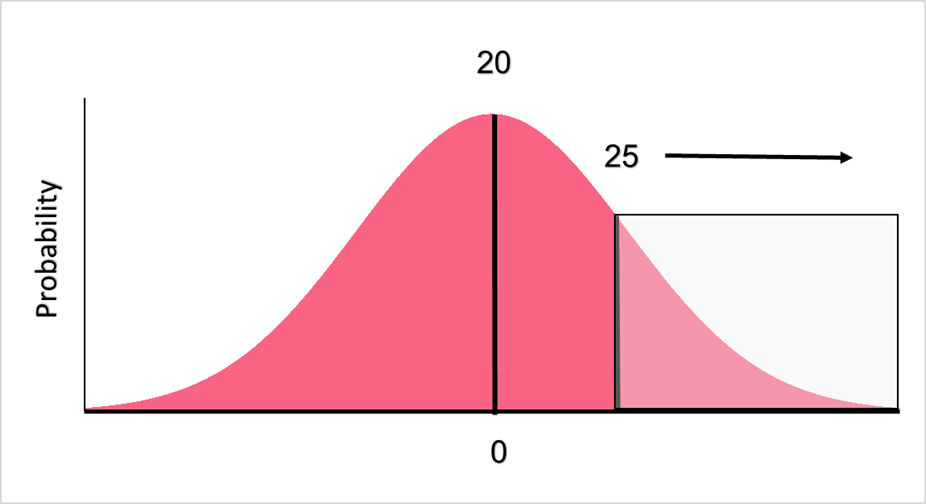
First we find the z-score.
\[
z-score = \frac{20-25}{1.5} = 3.33
\]
Next, we look at the z-table to find the probability.
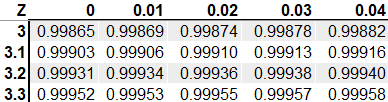
This gives us a probability of 0.0004, which is highly unlikely.













