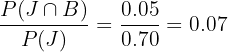In this article, you will learn how to solve word problems related to probability. So, let us get started.

Example 1
In a fruit basket, there are 12 apples, 13 strawberries, 20 cherries, and 7 bananas. Suppose a fruit is chosen at random from the basket. Calculate the probability of:
a) selecting a strawberry
b) selecting two bananas without replacement
c) selecting a strawberry and then a cherry
d) selecting a banana and then a cherry with a replacement
e) selecting three cherries at random
Solution
We will solve all the parts of this problem one by one.
Part a
Number of strawberries in the fruit basket = 13
Total number of fruits in the basket = 12 + 13 + 20 + 7 = 52
Probability of selecting a strawberry from the basket = 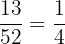
Part b
Number of bananas in the basket = 7
Total number of fruits in a basket = 52
Probability of selecting the first banana = 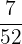
Probability of selecting the second banana = 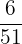
The probability of selecting two bananas without replacement = 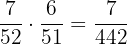
Part c
Total number of fruits in a basket = 52
Number of strawberries in the basket = 13
Probability of selecting a strawberry from the basket = 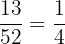
Probability of selecting a cherry after strawberry from the basket = 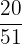
The probability of selecting a strawberry and then a cherry from the basket = 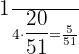
Part d
Total number of fruits in a basket = 52
Number of bananas in the basket = 7
Probability of selecting a banana in the basket = 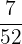
Note that the banana is replaced after picking up in this part.
Number of cherries in the basket = 20
Probability of selecting a cherry from the basket = 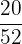
The probability of selecting a banana and then a cherry from the basket = 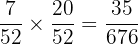
Part e
Total number of fruits in a basket = 52
Number of cherries in the basket = 20
Probability of selecting the first cherry = 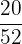
Probability of selecting the second cherry = 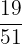
Probability of selecting the third cherry = 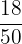
The probability of selecting three cherries = 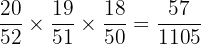
Example 2
In a group of 60 people, 28 have brown hair, 33 have brown eyes, and 13 have both brown hair and brown eyes. 12 people have neither brown eyes nor brown hair. Find the probability that a randomly selected person:
a) has brown hair only
b) has brown eyes only
c) has neither brown hair nor brown eyes
d) do not have brown eyes
e) do not have brown hair
f) has brown hair given that he/she has brown eyes
g) has brown eyes given that he/she has brown hair
Solution
In this example, we will solve each part one by one. But before proceeding to solve the example, we should make the Venn diagram first.

Part a
Total number of people in a group = 60
Number of people who have brown hair only = 15
Probability of selecting a person randomly who has brown hair only = 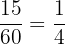
Part b
Total number of people in a group = 60
Number of people who have brown eyes only = 20
Probability of selecting a person randomly who has brown eyes only = 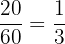
Part c
Total number of people in a group = 60
Number of people who have neither brown hair nor brown eyes = 12
Probability of selecting a person randomly who has neither brown eyes nor brown hair = 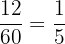
Part d
Total number of people in a group = 60
Number of people who have brown hair only = 15
Number of people who have neither brown eyes nor brown hair = 12
Number of people who do not have brown eyes = 15 + 12 = 27
Probability of selecting a person randomly who do not have brown eyes = 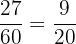
Part e
Total number of people in a group = 60
Number of people who have brown eyes only = 20
Number of people who have neither brown eyes nor brown hair = 12
Number of people who do not have brown hair = 20 + 12 = 32
Probability of selecting a person randomly who do not have brown hair = 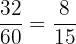
Part f
Number of people who have brown eyes and brown hair = 13
Probability of selecting a person randomly who has brown hair and brown eyes = 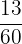
Number of people who have brown eyes only = 20
Probability of selecting a person randomly who has brown eyes = 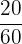
Probability of selecting a person at random who has brown hair given that he/she have brown eyes = P(A|B) = 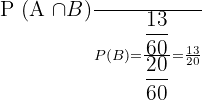
Part g
Number of people who have brown eyes and brown hair = 13
Probability of selecting a person randomly who has brown hair and brown eyes = 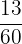
Number of people who have brown hair = 15
Probability of selecting a person randomly who has brown hair = 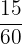
The probability of selecting a person randomly who has brown eyes given that he/she has brown hair = P(B|A) = 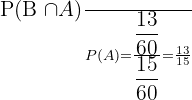
Example 3
There are four packets of chocolates. Each box has 45 chocolates in it. There are 25 dark chocolates in the first bag, 15 in the second bag, 35 in the third bag, and 10 in the fourth bag. Find the probability of selecting a dark chocolate from one of the four bags at random.
Solution
Total number of boxes = 4
Number of box selected = 1
Probability of selecting a box = 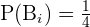
Total number of chocolates in the first bag = 45
Number of dark chocolates = 25
Probability of choosing a dark chocolate from the first bag = 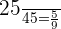
Total number of chocolates in the second bag = 45
Number of dark chocolates in the second box = 15
Probability of choosing a dark chocolate from the second box = 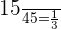
Total number of chocolates in the third box = 45
Number of dark chocolates in the third box = 35
Probability of choosing a dark chocolate from the third bag = 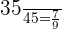
Total number of chocolates in the fourth box = 45
Number of dark chocolates in the fourth box = 10
Probability of choosing a dark chocolate from the fourth box = 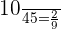
The probability of choosing the dark chocolate from one of the four boxes randomly will be calculated using the total probability rule.
P (dark chocolate) = 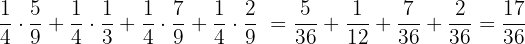
Example 4
If two dice are rolled simultaneously, what is the probability of obtaining a number less than 4 on the first die and a number greater than 4 on the second die?
Solution
Number of outcomes in the first die = 1, 2, 3 = 3
Total number of outcomes in the first die = 6
Probability of getting a number less than 4 on the first die = 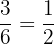
Number of outcomes on the second die = 5, 6 = 2
Total number of outcomes on the second die = 6
Probability of getting a number greater than 4 on the second die = 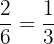
The probability of getting a number less than 4 on the first die and greater than 4 on the second die = 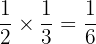
Example 5
70% of the people in a certain area do jobs. 20% of the people have businesses, while 5% do a job and have business. For a randomly selected person, calculate the probability that the person has his/her own business, given that he/she is doing a job?
Solution
Probability of randomly selected person doing a job = P(J) = 0.70
Probability of randomly selected person doing a job and having a business = 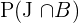 = 0.05
= 0.05
The probability of randomly selected person having his/her own business, given that he/she is doing a job = P (B|J) =