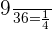Chapters
In this article, we will discuss what is probability and how to calculate it using its formulas.
The probability of an event is defined as the possibility of the occurrence of an event.
In other words, we can say that probability is a branch of mathematics that tells us the chances of an occurrence of an event in numerical form. The formulas of probability are quite useful in calculating the likelihood of the occurrence of an event. The probability of an event always has a value between 0 and 1. Zero probability means that it is impossible for an event to occur, whereas the probability of 1 means that there is a 100% chance that an event will happen.
If the probability of an event to occur is equal to a, then the probability of not occurring will be 1 - a. To calculate the chances of the occurrence of an event, we use probability formulas which we will discuss in the next section.

Probability Formulas
We know that probability measures the chances of the occurrence of an event. Today, the probability is widely used in fields such as commerce, biological science, medical sciences, and weather forecasting. To determine the chances of the occurrence of an event, you should know the total number of possible outcomes.
For instance, when you roll a dice on the floor, then the total number of possible outcomes is 6. If you want 5 to come, then your favorable outcome will be 5. The number of favorable outcomes in the case of 5 will be 1. If you want the numbers greater than 4, then the favorable outcomes will be 5 and 6. In this case, the number of favorable outcomes will be 2. The general formula for computing the probability of an event is given below:

Other Formulas of Probability
Some other formulas of probability are discussed below:
Probability Rule of Addition
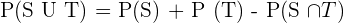
Mutually Exclusive Events
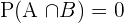
Independent Events
If A and B are independent, then their probability will be calculated using the following formula:
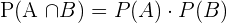
Conditional Probability
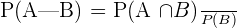
In the next section, we will solve some examples in which we will use the formulas discussed above.
Example 1
There are 13 colored pencils in a bag. 5 of them are red, 6 are blue, and the remaining are white.
a) What is the probability that a randomly selected pencil is red?
b) What is the probability that a randomly selected pencil is red and white?
c) What is the probability that a randomly selected pencil is red or blue?
Solution
Part a
Number of red pencils in the bag = 5
Total number of pencils in a bag = 13
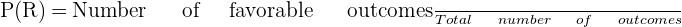
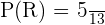
Part b
Number of red pencils in the bag = 5
Number of white pencils in the bag = 2
We cannot select both pencils at a time. Hence, both events are mutually exclusive.
Probability of selecting red and white pencil = 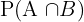 = 0
= 0
Part c
Number of red pencils in a bag= 5
Number of white pencils in a bag = 2
Total number of pencils in the bag = 13
Probability of selecting a red pencil = P(R) = 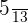
Probability of selecting a white pencil = P(W) = 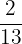
Probability of selecting red or white pencil = P (RUW) = 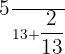
= 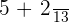
= 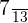
Example 2
Solution
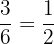


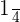
Example 3
In an area, 32% of the children play football and badminton. 68% of the children play badminton only. What is the probability of a child playing football given that he/she already plays badminton?
Solution
Percentage of the children who play both football and badminton = 32%
Probability of children who play both football and badminton= P(F and B) = 0.32
Percentage of children plating a badminton only = 68%
The probability of children playing badminton only = P(C) = 0.68
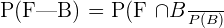
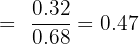
Example 4
What is the probability of selecting two even-numbered cards from the deck of 52 cards?
Solution
First, we will see what types of cards are present in each deck. The attributes of the deck of 52 cards are explained below:
- Each suit of the deck has 13 cards and a deck has 4 suits.
- Two are black cards and two are red.
- There are 13 cards in each suit which include a king, a queen, a jack, ace, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
In each suit, there are five even numbers 2, 4, 6, 8, and 7. Hence, in four suits, there will be 20 cards
Number of even-numbered cards in a deck = 20
Total number of cards in a deck = 52
The probability of selecting an even-numbered card from a deck = 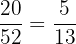
Now, we will calculate the probability of picking up the second even-numbered card from the deck.
Number of even-numbered cards left in a deck = 19
Total number of cards left in a deck = 51
The probability of drawing an even number card, given an even number card has already been drawn = 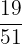
In this problem, we need to compute the probability of picking up two even number cards, therefore we will multiply the probabilities we have calculated above:
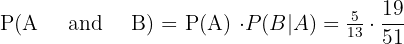
= 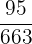
Example 5
A dice is rolled 4 times. What is the probability of getting 4 consecutive fours?
Solution
Probability of getting four single time = 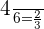
Probability of getting 4 four times = 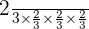
= 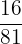
Example 6
Two dice are rolled on the floor. What is the probability of getting even numbers on both the dice?
Solution
Total number of outcomes = 6 x 6 = 36
Sample space = S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2), (4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }
Let A be an event in which both the dice have even numbers.
The number of possible outcomes will be 9
(2,2), (2, 4), (2, 6), (4,2), (4,4), (4,6), (6,2), (6,4), (6,6)
Probability of getting even numbers on both the dice = P(A) =