Chapters
In this article, you will find some of the solved examples of simple and compound probability. But before proceeding to solve the problems, first, you will get a short introduction to simple and compound probabilities and their formulae. So, let us get started.

What is Probability?
A likelihood of an event to occur or the extent to which something can happen is known as probability.
The definition of probability in mathematics is also the same. It is the likelihood of an event to occur. Few examples of probability are given below:
- Selecting a red ball from a group of colored balls
- Tails up after tossing a coin
- Selecting a queen card from the deck of 52 cards
- Choosing a chocolate-flavored ice cream from a set of eight flavors
These are only some of the examples of probability from our daily lives. The probability of the occurrence of different events vary.
- If it is certain that an event will occur, then its probability will be 1.
- If the probability of an event is 0, then we assume that there is no possibility of occurrence of an event.
- The probabilities of all possible events lie between 0 to 1.
We can denote this like this:
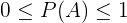
Here:
A is the event and P(A) is the probability of the occurrence of an event A. A sample space is the set of probable outcomes of an event. For example, if you toss two coins simultaneously, then the possible outcomes will be:
{(H,H), (H,T), (T,H), (T,T)}
This list of possible outcomes is known as sample space.
Finding a simple probability is straightforward as we just have to divide the number of ways in which an event can occur by the total number of outcomes.
Compound Probability
We use the following formula of compound probability if we are asked to tell the probability of the occurrence of more than one event:
P(A or B) = P(A) + P(B) - P(A and B)
Here:
- A and B are any two events.
- P(A) means the likelihood of the occurrence of event A.
- P(B) means the likelihood of the occurrence of an event B.
- P(A and B) is the probability that both the events A and B will occur at the same time.
Now, you know what the simple and compound probabilities are, let us proceed to the following examples that will make the whole concept more clear.
Example 1
In a class, there are 30 girls and 15 boys. 20 of the 30 girls like football and the rest of them like badminton. 10 of the 15 boys like football and the rest of them like badminton. Find the probability that the student selected randomly will be:
- A girl
- A boy who likes football
- A girl or a boy
Solution
There are three parts of this problem. We will find the probability of each event separately:
a) A girl
Number of girls in the class = 30
Total number of students in the class = 45
The probability that random students selected will be a girl = 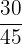
We will write the fraction in its most simplified form like this:
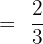
b) A boy who likes football
Number of boys who like football = 10
Total number of students in the class = 45
The probability that the student selected randomly will be a boy who likes football = 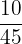
Simplifying the above probability will give us the following fraction:
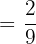
c) A boy or a girl
The probability that the selected student will be a boy or a girl is 1 because as we discussed earlier that if it is certain that an event will occur then the probability is 1.
Example 2
John rolls a dice. What is the probability of getting 3 or 6?
Solution
This is an example of a compound probability because we are asked to tell the probability of two events. The formula for computing the compound probability is given below:
P(A or B) = P(A) + P(B) - P(A and B)
According to this formula, first, we need to get the probability of each event separately like this:
Probability of getting 3 on the dice = 
Probability of getting 6 on the dice = 
Since only one dice is rolled, hence the probability of getting 3 and 6 both is 0.
Substituting the values of probability in the compound probability formula will give us the probability of getting 3 or 6:
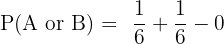
= 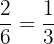
Example 3
Find the probability of selecting a red card or 2 from a deck of 52 cards.
Solution
To solve the questions of probability that are related to cards, you should know how 52 cards in a deck are distributed.
In a deck of 52 cards:
- There are four suits
- Two suit have black cards and two of them are red
- In each suit, there are 13 cards. These 13 cards include a queen, a king a jack, ace, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
Total number of red cards in a deck = 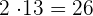
Total number of cards in a deck = 52
The probability of choosing a red card from the deck = 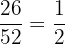
Number of cards having 2 in a deck = 4
Total number of cards in a deck = 52
Probability of choosing a 2 from a deck = 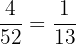
Total number of cards in a deck = 52
Number of red cards and 2 from a deck = 2
Probability of selecting a 2 and red card = 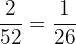
Now, we will substitute all these values in the compound probability formula to get the probability of selecting a red card or 2 from the deck.
P(A or B) = P(A) + P(B) - P(A and B)
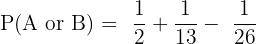
Solving and simplifying the above expression algebraically will give us the following answer:
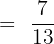
Example 4
In a pool, there are 20 balls and 40 blocks. 10 of the 20 balls are red and the rest of them are blue. 15 of the 45 blocks are green, 10 are red, and the rest of them are blue. Find the probability that the item picked randomly will be:
- A ball
- A ball of red color
- A blue-colored object
Solution
There are three parts of this problem. We will find the probability of each event separately:
a) A ball
Number of balls in the pool = 20
Total number of items in the pool = 60
The probability that a random item picked will be a ball:
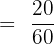
We will write the fraction in its most simplified form like this:
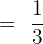
b) A ball of red color
Number of balls of red color= 10
Total number of items = 60
The probability that the randomly selected item will be a ball of red color = 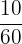
Simplifying the above probability will give us the following fraction:
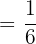
c) A blue-colored object
Number of blue balls in the pool = 10
Number of blue blocks in the pool = 20
Total number of objects in the pool = 60
Probability that the randomly selected item will be a blue-colored item = 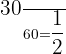
Example 5
Alice rolls a dice on the floor. What is the probability that the number will be a multiple of 2?
Solution
In the dice, there are six numbers {1, 2, 3, 4, 5, 6}. There are three multiples of 2 that are 2, 4, and 6.
Number of multiples of 2 on the dice = 3
Total numbers on the dice = 6
The probability that a number will be a multiple of 2 = 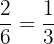 .
.













