
Normal Approximation to Binomial
Normal approximation refers to the approximation of continuous or normal distribution to a discrete or binomial distribution
The Central Limit Theorem says that for a larger sample the sampling distribution sample means becomes almost normal. Hence, for normal approximation to binomial, you must ensure that the sample size is large enough. But the questions arises, how to figure out that the sample is large enough and is fit for normal approximation to binomial? Well, we have explained this below:
First, you should know that two calculations n * p and n * q are used to figure out whether the sample size is large enough or not. Here, n represents the sample size, p is the given probability and q is equal to 1 - p.
For instance, lets assume that the probability is 0.7. We can find q by subtracting probability p from 1 like this:
q = 1 - p
q = 1 - 0.7
q = 0.3
Expressing these probabilities as percentages help us to understand the scenario quickly. If there is a 70% chance that you will go to the party (p), then there is a 30% probability that you won't go (q).
If n * p and n*q are greater than 5, then you can assume that the sample size is large enough to be used for normal approximation to binomial.
Mathematical Notation
We have already discussed in detail that when we can approximate the normal distribution to a binomial distribution. Mathematically, we can summarize all the details like this:
If  and
and 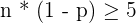 , then the normal distribution can be used to approximate the binomial distribution B(n, p).
, then the normal distribution can be used to approximate the binomial distribution B(n, p).
Example 1
Thirty five percent of students in a school are registered in the sports club. If a sample size of 800 students of a school is selected, find the probability that at least 250 are registered in the sports club.
Solution
Follow these steps to find the solution to this problem.
Step 1 - Find n, p, and q
In this step, we will find n, p, and q from the problem.
- It is given that thirty five percent of students are enrolled in the sports club. It means that the probability p is 35% or 0.35.
- To find q, we will subtract 0.35 from 1. q = 1 - 0.35 = 0.65
- The sample size n in this question is 800
Step 2 - Determine whether the sample size is large enough
In this step, we will determine whether the sample size is large enough to be used to approximate normal distribution to binomial distribution. Remember that to do so, we should ensure that n * p and n * q are greater than or equal to 5.
n * p = 800 * 0.35 = 280
n *q = 800 * 0.65 = 520
Both n * q and n * p are greater than 5, hence we can say that the sample size is large enough to be used to approximate normal distribution to binomial distribution.
Step 3 - Find the mean
Find the mean  by simply multiplying n with p. We have already calculated n * p in the previous step which is 280. Hence,
by simply multiplying n with p. We have already calculated n * p in the previous step which is 280. Hence, 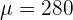 .
.
Step 4 - Multiply mean with q
Multiply mean 280 with q.
280 * 0.65 = 182
Step 5 - Find the standard deviation
Find the standard deviation by taking a square root of step 3. Remember that for a binomial distribution, the formula for standard deviation is 
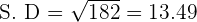
Step 6 - Write the Problem in mathematical notation
It is given that we need to find the probability that at least 250 students are registered in a sports club. Hence, we can write the probability as:
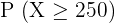
Step 7 - Rewrite using the continuity correction factor
Rewrite the problem using the continuity correction factor like this:
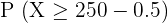
Step 8 - Find the z-score
Find the z-score by substituting the values of mean, x, and standard deviation in the following formula:
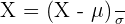

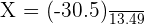
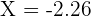
Step 9 - Use the z-table to find the value
In this step, we will use the z table to find the probability value. To do so, we will see the junction of row 2.2 and column 0.06.
P = 1 - 0.0119 = 0.9881
Hence, the probability that at least 250 students are registered at a sports club is 98.81%.
Example 2
In a particular city, one in four families owns a car. If 100 families are chosen at random, calculate the probability that at least 25 of them will have a car.
Solution
Follow these steps to find the solution to this problem.
Step 1 - Find n, p, and q
In this step, we will find n, p, and q from the problem.
- It is given that one in four families own a car. It means that the probability p is 25% or 0.25.
- To find q, we will subtract 0.25 from 1. q = 1 - 0.25 = 0.75
- The sample size n in this question is 100
Step 2 - Determine whether the sample size is large enough
In this step, we will determine whether the sample size is large enough to be used to approximate normal distribution to binomial distribution. Remember that to do so, we should ensure that n * p and n * q are greater than or equal to 5.
n * p = 100 * 0.25 = 25
n *q = 100 * 0.75 = 75
Both n * q and n * p are greater than 5, hence we can say that the sample size is large enough to be used to approximate normal distribution to binomial distribution.
Step 3 - Find the mean
Find the mean  by simply multiplying n with p. We have already calculated n * p in the previous step which is 25. Hence,
by simply multiplying n with p. We have already calculated n * p in the previous step which is 25. Hence, 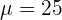 .
.
Step 4 - Multiply mean with q
Multiply mean 25 with q.
25 * 0.75 = 18.75
Step 5 - Find the standard deviation
Find the standard deviation by taking a square root of step 3. Remember that for a binomial distribution, the formula for standard deviation is 
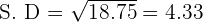
Step 6 - Write the Problem in mathematical notation
It is given that we need to find the probability that at least 25 families own a car. Hence, we can write the probability as:

Step 7 - Rewrite using the continuity correction factor
Rewrite the problem using the continuity correction factor like this:

Step 8 - Find the z-score
Find the z-score by substituting the values of mean, x, and standard deviation in the following formula:
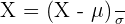
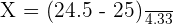
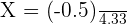

Step 9 - Use the z-table to find the value
In this step, we will use the z table to find the probability value. To do so, we will see the junction of row -0.1 and column 0.01.
P = 1 - 0.454 = 0.544
Hence, the probability that at least 25 families own a car is 54.4%.













It is a vey good resources. I has a few problems of not showing parenthesis at the correct place. Those can be corrected easily.
Thank you so much for your feedback! 😊 We’re glad you found the resource helpful. We appreciate you pointing out the issue with the parentheses — we’ll review and fix those right away. Your input helps us keep improving!
Iam unable to understand
I specified that I wanted 7th-grader stuff but these are not even in my whole textbook
Someone relook at the examples. What z table are you referring to? Once you solve for the Z the rest of the answer is gibberish. Maybe sh o w the table, label the axes and red line the values you call out so the student can figure out what you are trying to convey.
Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian