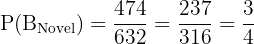Introduction
Probability is the branch of mathematics that deals with calculating the likelihood of a given event's occurrence, which we express as a number between 0 and 1.
- An event with a probability of 0 is an impossible event.
- An event with a probability of 1 is a certain event.
In word problems, our first step is always to determine the total number of possible outcomes (this is called the sample space). Then, we identify the number of outcomes that match the specific event we are interested in (the favourable outcomes).
The basic formula for the probability of an event, P(A), is:
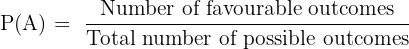
Problems become more interesting when we look at how different events relate to one another. There are three key types of relationships you need to know:
1. Mutually Exclusive Events
Two events are mutually exclusive if they cannot happen at the same time. For example, you cannot turn left and turn right simultaneously.
Rule: To find the probability of either event A or event B happening, you add their probabilities.
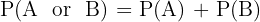
2. Independent Events
Two events are independent if the result of one does not affect the result of the other. For example, flipping a coin does not affect the roll of a die.
Rule: To find the probability of event A and event B both happening, you multiply their probabilities.
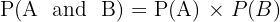
3. Conditional Probability
This applies when the probability of one event depends on another event having already happened. This is often written as P(A|B), which means "the probability of A given B".
For example, if you pick a card from a deck and do not put it back, the chance of picking a specific second card changes because there are fewer cards left.
Rule:
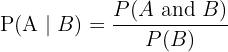
Worked Example
Problem:
In a survey of 100 students at a UK college, the following data was collected about their study choices:
- 40 students study Mathematics.
- 35 students study Science.
- 15 students study both Mathematics and Science.
A student is selected at random from the group.
- Represent this information on a Venn diagram.
- Find the probability that the selected student studies only Mathematics.
- Find the probability that the selected student studies neither Mathematics nor Science.
Solution:
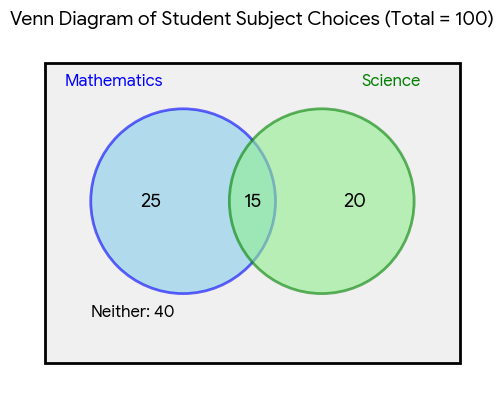
Part 1: The Venn Diagram
A Venn diagram is the perfect tool to visualise overlapping groups.
- We draw a box to represent all 100 students (the sample space).
- We draw two overlapping circles: one for Mathematics (A) and one for Science (B).
- Crucially, we always fill the intersection first. 15 students study both, so we place 15 in the central region where the circles overlap.
- Mathematics only: The total for the Mathematics circle is 40. We have already accounted for 15 in the intersection. So, those studying only Mathematics are:
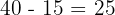
- Science only: The total for the Science circle is 35. We have already accounted for 15 in the intersection. So, those studying only Science are:
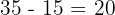
- Finally, we find the number of students who study neither subject. We add up everyone inside the circles and subtract this from the total number of students:
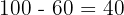
This number goes outside the circles but inside the box. The completed Venn diagram visualises these four distinct groups: Math only (25), Science only (20), Both (15), and Neither (40).
Part 2: Probability of studying only Mathematics
The total number of possible outcomes is the total number of students, which is 100.
From our Venn diagram calculation, the number of students studying only Mathematics is 25.
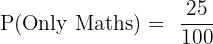
Simplifying the fraction:
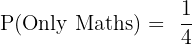
Part 3: Probability of studying neither subject
Again, the total number of outcomes is 100.
From the Venn diagram, the number of students in the "neither" region is 40.
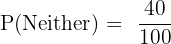
Simplifying the fraction:
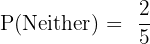
Practice Problems & Solutions
In a class where every student plays at least one sport, it is known that: 60% of students play football, 50% of students play basketball, 10% of students play both football and basketball.
Calculate the probability that a student chosen at random from the class:
- Plays only football.
- Plays only basketball.
- Plays only one of the sports.
Since every student plays at least one sport, there is no one in the "neither" category. We can use a Venn diagram approach with percentages.
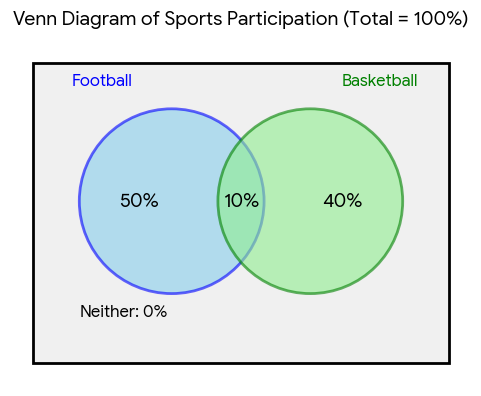
a. Plays only football: The total percentage for football is 60%. This includes the 10% who play both. Percentage for only football = Total football - Both
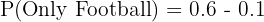
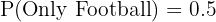
b. Plays only basketball: The total percentage for basketball is 50%. Percentage for only basketball = Total basketball - Both
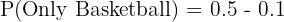
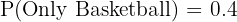
c. Plays only one of the sports: This is the sum of those who play only football and those who play only basketball.
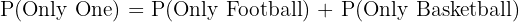
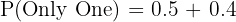
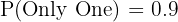
In a city, the following probabilities have been determined about the population:
Probability of having brown hair, P(H) = 0.4, probability of having brown eyes, P(E) = 0.25, and probability of having both brown hair and brown eyes P(H and E) = 0.15
A person is chosen at random.
- Given that the person has brown hair, what is the probability that they also have brown eyes?
- What is the probability that the person has neither brown hair nor brown eyes?
a. This question asks for a conditional probability:
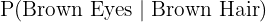 .
.
The formula is:
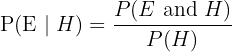
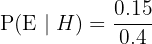
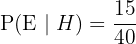
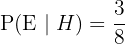
b. Probability of "Neither":
First, we find the probability of a person having either brown hair or brown eyes using the addition rule:
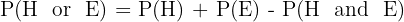
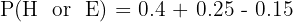
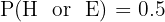
The probability of having "neither" is the complement of having "either".
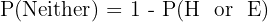
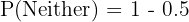
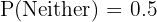
There are two boxes containing coloured balls:
Box A: 6 red balls and 4 blue balls (Total = 10).
Box B: 4 red balls and 8 blue balls (Total = 12).
A standard six-sided die is rolled. If the roll is 1 or 2, a ball is selected from Box A. If the roll is 3, 4, 5, or 6, a ball is selected from Box B.
Calculate:
- The probability that the selected ball is red and from Box B.
- The total probability that the selected ball is blue.
a. This is a compound event involving two independent stages: rolling the die, then picking a ball.
Probability of selecting Box B (rolling 3, 4, 5, or 6):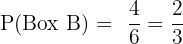
Probability of picking a red ball from Box B: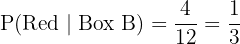
We multiply the probabilities of these two events:
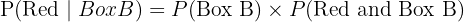
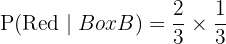
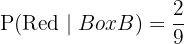
b. A blue ball can be chosen in two ways:
Way 1: Select Box A and then pick a blue ball.
Probability of Box A: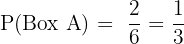
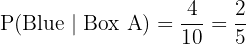
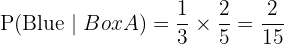
Way 2: Select Box B and then pick a blue ball.
Probability of Box B: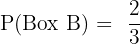
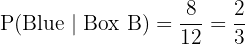
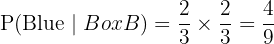
These two ways are mutually exclusive, so we add their probabilities:
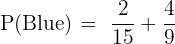
To add them, find a common denominator (45):
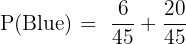
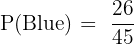
A student has an alarm clock that successfully wakes him 80% of the time. If he wakes up on time, the probability he writes his test is 0.9. If he does not wake up on time, the probability he writes his test is only 0.5.
Calculate the probability that:
- He wakes up on time and writes the test.
- He does not write the test.
a. Wakes up and writes the test:
We multiply the probability of the first event by the conditional probability of the second.
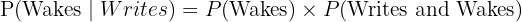
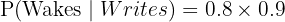
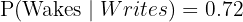
b. Does not write the test:
There are two ways to not write the test:
Way 1: He wakes up but does not write the test.
Probability he does not write given he wakes:
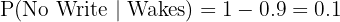
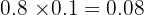
Way 2: He does not wake up and does not write the test.
Probability he does not wake:
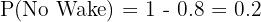
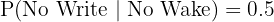
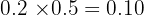
Add the probabilities of these two mutually exclusive scenarios:
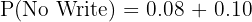
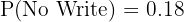
On a shelf, there are 60 novels and 20 poetry books (Total = 80 books). Person A chooses a book at random and leaves with it. Then, Person B chooses another book at random from the remaining ones. Calculate the probability that:
- Person A chooses a novel and Person B chooses a poetry book.
- The book selected by Person B is a novel.
This is a problem involving dependent events (sampling without replacement).
a. A gets Novel, B gets Poetry:
Probability A gets a Novel:
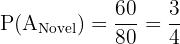
After A takes a novel, there are 79 books left: 59 novels and 20 poetry books.
Probability B gets a Poetry book (given A took a novel):
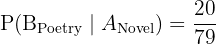
Multiply the probabilities:
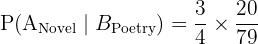
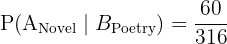
Simplifying the fraction (divide by 4):
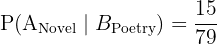
b. B gets a Novel: This can happen in two ways:
Way 1: A gets a Novel, then B gets a Novel.
First probability:
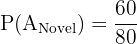
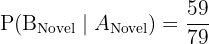
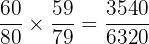
Way 2: A gets a Poetry book, then B gets a Novel.
First probability: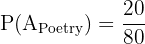
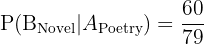
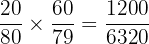
Add the probabilities:
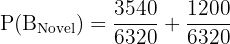
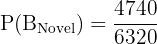
Simplifying the fraction (divide by 20, then by 4, then by 79):