Chapters

What is a Standard Normal Distribution?
A normal distribution with a mean of zero and a standard deviation of one is known as a standard normal distribution.
It is centered at zero and it gives the extent to which the given measurement deviates from the mean. In a standard normal distribution:
- 68% of the observations fall within 1 standard deviation of the mean
- 95% of the observations fall within 2 standard deviations of the mean
- 99.9% fall with 3 standard deviations of the mean
The standard normal distribution is also referred to as z-distribution. We generally use X to represent our variable of interest, for instance, height = X, and age = X, etc. However, in the standard normal distribution, we use Z. We can standardize any normal distribution by transforming its values into z-scores. A z-score of the value tells us the number of standard deviations the value lies away from the mean.
Difference between Standard Normal and Normal Distributions
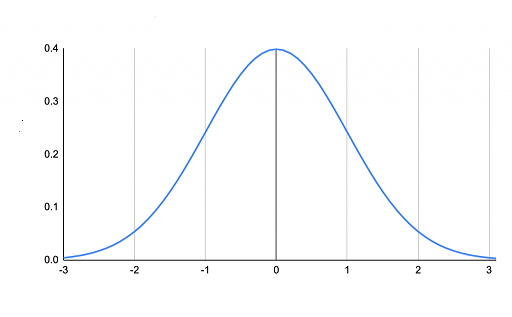
We know that all normal distributions are unimodal and they are distributed symmetrically in the form of a bell-shaped curve. The same is the case with standard normal distribution. The difference between a normal distribution and standard normal distribution is that a normal distribution can take on any value as its mean and standard deviation. On the other hand, a standard normal distribution has always the fixed mean and standard deviation.
Each normal distribution is a kind of a standard normal distribution that is elongated or squeezed and moved horizontally in the right or left direction. The mean in the standard normal distribution tells us where the curve is centered. If the mean is increased, the curve will move to the right. In contrast, if the mean is decreased, the curve will move to the left. The standard deviation either stretches or squeezes the curve. A narrow curve represents that the standard deviation is small, whereas a wider curve represents a large standard deviation.
Density Function of Standard Normal Distribution
The standard normal distribution has a mean of zero, i.e. 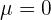 , and a standard deviation of 1, i.e.
, and a standard deviation of 1, i.e.  . Its density function is given below:
. Its density function is given below:

Its graph is given below:
Standard Score or Z score
A standard score or a z-score refers to the normal random variable of the standard normal distribution. All normal random variables X can be converted into a Z-score using the following formula:

In the next section of the article, we will solve some examples related to standard normal distribution.
Example 1
Sam got a 750 score in the annual exam. The mean exam score of the class was 600 with a standard deviation of 120. Suppose that the exam scores were normally distributed. What proportion of students achieved a higher score than Sam?
Solution
Sam score in the exam = X = 750
Mean score =  = 600
= 600
Standard deviation =  = 120
= 120
Use the following formula to calculate the Z-score or standard score:

Substitute the values of X,  , and
, and  in the above formula to get the z-score:
in the above formula to get the z-score:

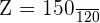
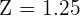
Now, we will use the Z-table to find the probability P(Z > 1.25). To do so, we will see where the number 1.2 in the row overlaps with column 0.05. From the table, we got the value 0.8944. Remember that it represents P(Z<1.25). To find the greater than value, we will subtract this probability from one.
= 1 - 0.8944
= 0.1056 or 10.56%
Hence, we can say that approximately 10.56% of the students achieved a higher score than Sam.
Example 2
The monthly income of Mariah is \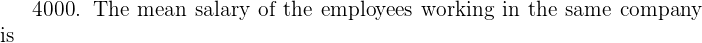 3800 with a standard deviation of \
3800 with a standard deviation of \ 4000
4000
Mean salary =  = \
= \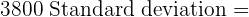 \sigma
\sigma 400
400
Use the following formula to calculate the Z-score or standard score:

Substitute the values of X,  , and
, and  in the above formula to get the z-score:
in the above formula to get the z-score:

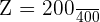
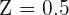
Now, we will use the Z-table to find the probability P(Z > 0.5). To do so, we will see where the number 0.5 in the row overlaps with column 0.00. From the table, we got the value 0.6915. Remember that it represents P(Z<0.5), but we have to calculate P(Z>0.5). To find the greater than value, we will subtract this probability from one.
= 1 - 0.6915
= 0.3085 or 30.85%
Hence, we can say that approximately 30.85% of the employees earn more than Mariah.
Example 3
The number of days the athletes spend in training before the annual national event approximates a normal distribution with a mean of 210 days and a standard deviation of 12 days. What proportion of the athletes training lies between 220 to 250 days?
Solution
Mean =  = 210
= 210
Standard deviation =  = 12
= 12
To calculate the Z-score for 220 days, substitute X = 220,  = 280, and
= 280, and  = 12 in the formula below:
= 12 in the formula below:


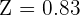
Now, we will calculate the Z-score for 250 days. To calculate the Z-score for 250 days, substitute X = 250,  = 210, and
= 210, and  = 12 in the formula below:
= 12 in the formula below:

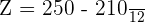

P(220 < X < 250) = P(0.83 < X < 3.33)
= P (Z < 3.33) - P(Z < 0.83)
= 0.9996 - 0.7967
= 0.2029
Hence, 20.29% of the athletes training fall between 220 to 250 days.
Example 4
Harry finds that his weight is 120 pounds. The mean weight of his fellow students in the class is 110 pounds with a standard deviation of 15. What proportion of students has less weight than Harry?
Solution
Harry's weight = X = 120 pounds
Mean weight =  = 110 pounds
= 110 pounds
Standard deviation =  = 15
= 15
Use the following formula to calculate the Z-score or standard score:

Substitute the values of X,  , and
, and  in the above formula to get the z-score:
in the above formula to get the z-score:
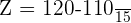
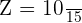
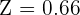
Now, we will use the Z-table to find the probability P(Z < 0.66). To do so, we will see where the number 0.6 in the row overlaps with column 0.06. From the table, we got the value 0.7454.
P(Z < 0.66) = 0.7454
= 74.54%
Hence, we can say that approximately 74.54% of the students weigh less than Harry.
Example 5
Alice takes 5 hours to complete her project. The average time taken by other students in the class to complete the same project is 7 hours with a standard deviation of 2.2. Assuming that the time taken by students to complete the project is normally distributed, what proportion of students took lesser time than Alice to complete the project?
Solution
Time taken by Alice to complete the project = X = 5 hours
Mean time =  = 7 hours
= 7 hours
Standard deviation =  = 2.2
= 2.2
Use the following formula to calculate the Z-score or standard score:

Substitute the values of X,  , and
, and  in the above formula to get the z-score:
in the above formula to get the z-score:
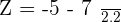
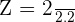
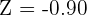
Now, we will use the Z-table to find the probability P(Z < -0.90). To do so, we will see where the number -0.9 in the row overlaps with column 0.00. From the table, we got the value 0.1841.
P(Z < -0.90) = 0.1841
= 18.41%
Hence, we can say that approximately 18.41% of the students took less time than Alice to complete the project.













It is a vey good resources. I has a few problems of not showing parenthesis at the correct place. Those can be corrected easily.
Thank you so much for your feedback! 😊 We’re glad you found the resource helpful. We appreciate you pointing out the issue with the parentheses — we’ll review and fix those right away. Your input helps us keep improving!
Iam unable to understand
I specified that I wanted 7th-grader stuff but these are not even in my whole textbook
Someone relook at the examples. What z table are you referring to? Once you solve for the Z the rest of the answer is gibberish. Maybe sh o w the table, label the axes and red line the values you call out so the student can figure out what you are trying to convey.
Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian