Chapters

Central Tendency Definition
| Population | Sample | |
| Definition | The entire group of things, ideas or places you want to study | A portion of the population used for estimating population measures |
| Example | All students in university in one country | A random sample of 2,000 university students |
| Measure | Population parameter | Sample statistic |
As you can see from the table above, when a measure is calculated from a sample, it is called a sample statistic. We typically deal with samples in statistics, as it is rare to have the true population parameter. The image below is an example that highlights the differences between the two measures.

Mean Definition
While there are many different measures in statistics, there are a couple of common measures that we use when analysing data. These are summarized in the table below.
| Measures of Central Tendency | Measures of Spread |
| Gives an idea of where the centre of all values is located | Gives an idea of the distribution of the values around the centre |
| Mean, median, mode | Variance, standard deviation, range, percentiles |
The graph below contains the mean and the range for a given variable. This serves to illustrate the main difference in these two types of measures. While the mean tells us about the average value of the variable, the range tells us if this variable varies by a lot or a little.

The mean is the most common measure of central tendency and is defined as a simple average of all values of a variable.
Mean Formula
To calculate the mean, you can follow the formula below.

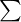 | The summation of all values |
 | The value of variable x for the ith observation |
| n | The sample size |
To understand this fully, take test scores as an example.
| Student Number | Test Score |
| 1 | 45 |
| 2 | 49 |
| 3 | 47 |
The mean of this sample size of three students is the following.

Confidence Interval Definition
To understand the confidence interval, recall from earlier in this section that we rarely have information about the population. We estimate the true population measures with sample statistics. One of the most common sample statistics is the mean, which is the average of a group of values. The confidence interval gives us a range of values which are one standard deviation above and below the mean, which represent the range of values we are almost sure the true population parameter lies within.

The picture above shows an example of a sample mean and the confidence interval for that mean.
Probability Distribution
In order to calculate the confidence interval of a sample mean, you should understand what a probability distribution is. The image below displays two common distributions used within probability.

A probability distribution is a graph that displays all values of a variable and the probability of each value occurring. For example, all possible heights between 140 and 200 cm, where the bell-shaped line represents the probability that someone is any given height. The graphs above show a standard normal distribution and a t-distribution whose sample size is above 30. The details of these two distributions are summarised below.
| Parameters | Variable | |
| Standard normal |  , ,  | Normal |
| Student’s t | df (degrees of freedom) | t-distribution |
Standard Normal Distribution
Here, we will use the standard normal distribution in order to discuss confidence intervals. Because we want to be sure that we are capturing the population parameter, we can use a standard normal distribution to calculate which range of values are most likely to capture the mean.

A standard normal distribution represents a mean represented by 0. This is because all the values of a variable have been standardised. Each line in the graph represents 1 standard deviation away from the previous line, starting with the mean. All of the values in the interval between -1 and 1 standard deviation represent a 68% probability.
| Probability | Combined Probability | Cumulative Probability | |
1,-1  | 34.1%, 34.1% | 68.2% | |
2,-2  | 13.6%, 13.6% | 27.2% | 95.4% |
3,-3  | 2.1%, 2.1% | 4.2% | 99.6% |
4,-4  | 0.2%, 0.2% | 0.4% | 100% |
We usually use the interval 2 SDs above and below the mean, because it captures about 95% of the values.
Z-score
In order to standardise all values of a variable, it is necessary to run them through a standardisation formula. The formula takes the plain number, known as a raw score, and converts it into a standardised value, known as a z-score. This formula is the following,
\[
z-score = \frac{x-\bar{x}}{s}
\]
Where x is the raw score,  is the mean and s is the sample standard deviation. This allows us to compare the raw scores in terms of the standard deviation. These standardised numbers always have the same probability because they are dependent on the z-score. The table below shows how different heights and SD’s result in the same probability when they have the same z-score.
is the mean and s is the sample standard deviation. This allows us to compare the raw scores in terms of the standard deviation. These standardised numbers always have the same probability because they are dependent on the z-score. The table below shows how different heights and SD’s result in the same probability when they have the same z-score.
| Raw Score | Mean | Standard Deviation | Z-score | Probability |
| 150 | 170 | 20 | 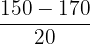 = 1 = 1 | 0.8413 |
| 180 | 160 | 60 | 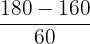 = 1 = 1 | 0.8413 |
Z-table
You may be wondering where we got the probabilities in the previous example. Because the probabilities correspond to the z-scores, they are written in a table called a z-table. This table is widely available online and in statistics books. An extract of a left-tailed table can be seen in the image below.

The ones place and tenths place in your z-score is first found on the left column, while the hundredths place is found in the first row. The intersection of these two are where the probability for your z-score is.
Confidence Interval Example with Standard Normal Distribution
Let’s continue our example from before and say you’re interested in finding the confidence interval of a sample mean height of 175 with a sample standard deviation of 10 with a sample size of 100. First, we look at the table below, which has the most common z-scores and their probabilities.
| Probability (Confidence Interval) | z-score |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
Next we use the formula for the confidence interval:

This gives us,
\[
175 \pm 1.96 \frac{10}{\sqrt{500}} = 173.04, 176.96
\]













