Chapters

Measures of Central Tendency
The measure of central tendency is a value that describes the data set by finding the central position within it. As measures of central tendency describe the central location of the data set, therefore they are also referred to as measures of central location. Summary statistics is another name given to these values. You may be familiar with the mean which is the most common kind of the measures of central tendency and represents the average value of the data set. The mode, median, and range are all the measures of central tendency, however we use these according to the circumstances. In this article, we will discuss the mode in detail.
What is Mode?
The mode is one of the measures of central tendency that reflects the most repeated value in a data set. It is denoted by 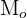 . We can find modes for categorical and quantitative variables. The data can be distributed in numerous ways in statistics. The most common distribution is the normal distribution in which the data is distributed in the form of a curve. In some distributions including the normal one, the mean that gives the average value lies at the mid-point. The mean gives the peak frequency of all the observed values. In this scenario, the mean, median and mode all are equal, i.e. they have the same values. It means the mode in such distribution gives us valuable information about the average value, middle value, and the most repeated value.
. We can find modes for categorical and quantitative variables. The data can be distributed in numerous ways in statistics. The most common distribution is the normal distribution in which the data is distributed in the form of a curve. In some distributions including the normal one, the mean that gives the average value lies at the mid-point. The mean gives the peak frequency of all the observed values. In this scenario, the mean, median and mode all are equal, i.e. they have the same values. It means the mode in such distribution gives us valuable information about the average value, middle value, and the most repeated value.
Now, we will see how to calculate the modes of the data set.
For instance, consider the following data set:
3, 3, 4, 3, 4, 2, 1, 1, 5, 6
Some of the digits are occurring more than once in the above data set. 3 is repeated three times, while 4 and 1 both are repeated two times. Since the mode is the most repeated value in the data set, therefore the mode in the above data set is 3. We will write it as:
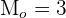
We can have a bimodal or multimodal data set. The bimodal data set means that the set has two modes. Having two modes means that in the set two values have the same maximum frequency. Frequency refers to the number of times an element is written in a data set. A multimodal data set has several modes in it.
For example, in the following data set 5 and 7 occur two times. Therefore, this data set has 2 modes and is termed as a bimodal data set.
5, 7, 3, 5, 7, 8, 9, 0
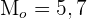
Consider another data set below:
1, 2, 4, 5, 1, 2, 5, 6
In the above data set, 1, 2 , and 5 are repeated 2 times. It means that the data set has multiple modes. We will write it as:

Have you ever wondered, what will be the mode of the data set in which all the elements have the same frequency? Well, there is no mode in this type of data set. For example, consider the following set in which all the elements are repeated twice.
2, 2, 3, 3, 4, 4, 5, 5
We can say that the frequency of all the elements in the above data set is the same, hence it has no mode.
There is another scenario, in which we are given a data set in which two adjacent values have the maximum frequency. In this case, the mode of the data set will be the average values of these two adjacent values. For example, consider the following data set:
1, 3, 4, 4, 6, 6, 8, 9
In the above data set, 4 and 6 have the same frequency and these values are written adjacent to each other. To find the mode of the data set, we will take an average of the middle two values, i.e. 4 and 6.

Calculation of the Mode for Grouped Data
Now, we will see how to calculate the mode for grouped data. For the grouped data, there are two scenarios:
- When all the classes have the same width
- When all classes have different widths
In the next section, we will see the formula for computing the mode of the grouped data when all the classes have the same width.
Calculation of Mode When All Classes Have the Same Width.
The formula for computing the mode of the grouped data when all classes have the same width is given below:
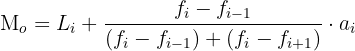
Here:
 refers to the lower limit of the modal class.
refers to the lower limit of the modal class.
 represents the absolute frequency of the modal class.
represents the absolute frequency of the modal class.
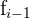 refers to the absolute frequency immediately before the modal class.
refers to the absolute frequency immediately before the modal class.
 represents the absolute frequency immediately after the modal class.
represents the absolute frequency immediately after the modal class.
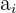 refers to the class width of the modal class
refers to the class width of the modal class
Note: the modal class means the class which has the highest frequency.
Example
Calculate the mode of a statistical distribution given by the following table:
| [43, 46) | 5 |
|---|---|
| [46, 49) | 18 |
| [49, 52) | 42 |
| [52, 55) | 27 |
| [55, 58) | 8 |
| 100 |
Solution
In this example:

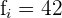
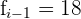


Substitute these values in the following formula to compute mode of statistical distribution for a grouped set when class widths are the same:
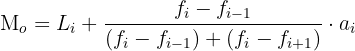
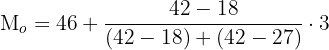
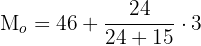

Calculation of Mode When All the Classes Have Different Widths.
In this section, we will see how to calculate the mode of the grouped data if all the classes have different widths. In this case, first, you need to compute the heights of all the classes by using the formula below:
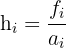
Here,  represents the frequency of the class, whereas
represents the frequency of the class, whereas 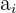 represents the width of the class. Use the formula below to compute modes of the grouped data when widths are different:
represents the width of the class. Use the formula below to compute modes of the grouped data when widths are different:
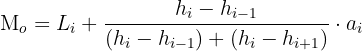
Here:
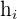 refers to the height of the modal class
refers to the height of the modal class
 represents the height of the class before the modal class
represents the height of the class before the modal class
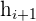 refers to the height of the class after the modal class
refers to the height of the class after the modal class
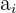 represents width of the modal class
represents width of the modal class
Example
The following table shows the score obtained by the group of 48 students. Calculate the mode.
| [0,5) | 15 | 3 |
| [5,7) | 20 | 10 |
| [7,9) | 10 | 5 |
| [9,10) | 3 | 3 |
Solution
First, we will identify the values from the above table.
The table shows the following values:
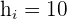
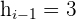
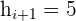
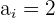
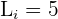
Substitute the above values in the formula below to calculate the mode:
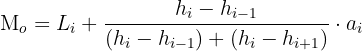
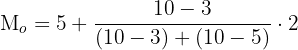


Hence, the mode of the grouped data is 6.16.













