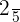Chapters
In mathematics, a probability refers to the likelihood of the occurrence of an event
In other words, we can say that probability is used to forecast the chances of an event to occur. Probability has many applications in the fields of commerce, physics, biological and medical sciences, and weather forecasting. In this article, we will discuss the important properties of probability in detail.

Properties of Probability
The properties of probability are discussed below:
- For an event A, its probability is defined as P(A). The probability of an event A is calculated by the following formula:
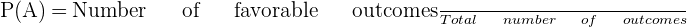
- If there is no ambiguity in the occurrence of an event, then the probability of such an event is equal to 1. In other words, the probability of a certain event is 1.
- If an event has no chances of occurring, then its probability is 0.
- The probability of an event A is depicted by a number P (A) in such a way that
 . In short, the probability is always a positive number.
. In short, the probability is always a positive number. - For two mutually exclusive events R and S, P(R U S) = P(R) + P(S).
- The event that has only one outcome is known as an elementary event. The sum of probabilities of elementary events is equal to 1.
- P (R U S) = P(R) + P(S) - P(R \cap S)
- P(R \cap S) = P(R) + P(S) - P(RUS)
- For mutually exclusive events
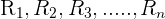 ,
,  is equal to
is equal to 
In the next section, we will solve some examples related to probabilities.
Example 1
What is the probability of getting a number greater than 4 when rolling a dice?
Solution
Number of favorable outcomes = (5,6) = 2
Total number of outcomes = 6

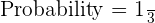
Example 2
If two dice are thrown simultaneously, then what is the probability of getting a number greater than or equal to 11?
Solution
Since two dice are thrown simultaneously, hence a total number of outcomes is equal to 6 x 6 = 36.
A total of 11 can be obtained as (5, 6) and (6, 5).
A total of 12 can be obtained as (6,6)



Example 3
From a deck of 52 cards, what is the probability of choosing a queen or a jack card?
Solution
These events are mutually exclusive because it is not possible to select two cards at the same time.
Number of queen cards in a deck = 4
Total number of cards in a deck = 52
The probability of selecting a queen card = 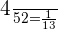
Number of jack cards in a deck = 4
Total number of cards in a deck = 52
The probability of selecting a jack card = 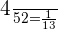
The probability of selecting a queen card or a jack = 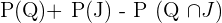
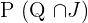 is 0.
is 0.
= 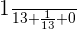
= 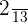
Example 4
If the probability of passing a test is 50% and not passing it is 20%, then find the following:
a) The probability of passing and not passing a test
b) The probability of passing or not passing a test
Solution
Part a
The probability of passing a test = P(A)
The probability of not passing a test = P(B)
The probability of passing and not passing a test = 
= 0
Part b
The probability of passing or not passing a test = P (A U B) = P(A) + P(B)
= 50% + 20%
= 70%
Example 5
There are 40 students in a class. 15 of the 40 students like mathematics and 35 of the 40 students like both mathematics and physics. If a student is chosen at random, what is the probability that he likes both mathematics and physics?
Solution
Suppose that the number of students who like both mathematics and physics is x.
Number of students who like mathematics only = 15 - x
Number of students who like physics only = 35 - x
There are 60 students in a class, hence we can write the equation as:
15 - x + x + 35 - x = 40
50 - x = 40
x = 10
The probability that a randomly chosen student like both the subjects = 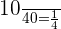
Example 6
Out of 150 students in a school, 80 play football, 30 play cricket, 20 play badminton and the remaining play no sport at all. What is the probability that a randomly chosen student:
a) plays football only
b) plays football or a badminton
c) plays neither badminton nor a football
Solution
Part a
Total number of students in a school = 150
Number of students who play football = 80
Probability that a randomly chosen student plays football only = 
Part b
Total number of students in a school = 150
Number of students who play football or badminton = 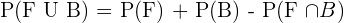
The probability of playing football and badminton = 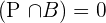
The probability of playing football or badminton = 
= 
= 
Part c
Probability of playing neither football nor a badminton = 1 - P(F U B)
= 
= 
Example 7
A bag contains 12 red and 8 green colored marbles. If one marble is chosen at random, what is the probability of choosing:
a) a red and green marble
b) a red or green marble
Solution
Part a
Total number of marbles in a bag = 20
Probability of choosing a red marble = P(R)
Probability of choosing a green marble = P(G)
Probability of choosing a red and a green marble = 
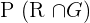 is 0 because the events are mutually exclusive.
is 0 because the events are mutually exclusive.
Part b
Total number of marbles in a bag = 20
Probability of choosing a red marble = P(R)
Probability of choosing a green marble = P(G)
Probability of choosing a red and a green marble = 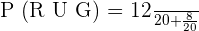
= 
= 1
Hence, the probability of choosing a red or a green marble is 1.
Example 8
The probability of selecting a bar of dark chocolate from a set of chocolates is  . What is the probability of not selecting a bar of dark chocolate?
. What is the probability of not selecting a bar of dark chocolate?
Solution
Probability of selecting a bar of dark chocolate = 
Probability of not selecting a bar of dark chocolate = 
= 
Example 9
The probability of selecting a red ball is 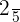 and the probability of selecting a green ball is
and the probability of selecting a green ball is 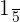 . What is the probability of not selecting either a red or a green ball?
. What is the probability of not selecting either a red or a green ball?
Solution
The probability of selecting a red ball = P (R) = 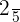
The probability of selecting a green ball = P (G) = 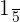
The probability of selecting a red or a green ball = P(R U G) = P (R) + P (G) = 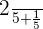
= 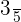
The probability of not selecting a red or a green ball = 
=