Chapters

What is Probability?
We know that probability in statistics refers to the likelihood of the occurrence of an event. If an event is certain, then its probability is equal to 1. The probability of an impossible event is zero.
Law of Total Probability
In probability theory, there is a basic rule that is related to the marginal and conditional probabilities. This rule is known as the law of total probability. Through this law, we can find out the total probability of events from many distinct events.
The law of total probability is also known as the total probability rule. It breaks down the probability computations into different parts. It is used to calculate the probability of an event, A when there is insufficient information about A's probabilities to calculate it directly. Instead of trying to calculate the probability of an event A directly, we take the probability of the related event B and utilize it to compute the probability of an event A.
The probability of event A can be written as an aggregate of event B. If 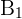 ,
,  , and
, and 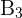 .... is a partition of the sample space S, then for any event A, the total probability rule is given by:
.... is a partition of the sample space S, then for any event A, the total probability rule is given by:
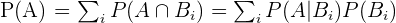
In the next section, we will calculate the probabilities using the total probability rule.
Example 1
A different number of light bulbs are present in three boxes. The first box has 12 bulbs, out of which 5 are dead. The second box has eight bulbs, out of which the dead ones are 3. The third box has nine bulbs, out of which two are dead. Find the probability of selecting a dead bulb randomly from one of the three boxes.
Solution
Total number of boxes = 3
The number of boxes from which the bulbs will be chosen = 1
Probability = P (B_i) = 
Total number of bulbs in the first box = 12
Number of dead bulbs = 5
The probability of choosing a dead bulb from the first box = 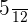
Total number of bulbs in the second box = 8
Number of dead bulbs = 3
Probability of choosing a dead bulb from the second box = 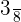
Total number of bulbs in the third box = 9
Number of dead bulbs = 2
Probability of choosing a dead bulb from the third box = 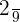
Probability of choosing the dead bulb from one of the three boxes will be calculated using the total probability rule.
P (dead) = 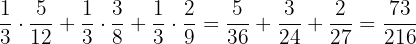
Example 2
Sam wants to travel to another city. The probabilities of going to another city on the pre-determined day with or without rain are 0.36 and 0.80 respectively. If the probability of rain on that day is 0.30, then determine the probability that Sam will go to another city on that day?
Solution
Suppose A be the event that Sam will go to another city on that day and B be the event that it rains. We have,
P(B) = 0.30
P(no rain) = P(B′) = 1 − P(B) = 1 − 0.30 = 0.70
The conditional probabilities of these events will be:
P(A|B) = 0.36
P(A|B') = 0.80
Because the events B and B' form the partitions of the sample space, S, hence, by the total probability theorem, we will calculate the probability like this:
P(A) = P(B) P(A|B) + P(B′) P(A|B′)
= 0.30 x 0.36 + 0.70 x 0.80
=0.108 + 0.56
= 0.668
Hence, the probability that it will rain on that day and Sam will go to another city is 0.668 or 66.8%.
Example 3
There are three groups in the class. Each group contains a different number of students. The first group has 15 students, out of which 8 are girls. The second group has 9 students, out of which the girls are 4. The third group has 12 students, out of which 7 are girls. Find the probability of selecting a girl randomly from one of the three groups.
Solution
Total number of groups = 3
The number of groups from which a girl will be selected = 1
Probability = P (B_i) = 
Total number of students in the first group = 15
Number of girls = 8
Probability of choosing a girl from the first group = 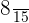
Total number of students in the second group = 9
Number of girls in that group = 4
Probability of choosing a girl from the second group = 
Total number of students in the third group = 12
Number of girls in the third group = 7
Probability of choosing a girl from the third group = 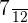
The probability of choosing the girl from one of the three groups will be calculated using the total probability rule.
P (girl) = 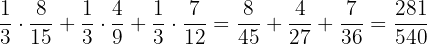
Example 4
There are four bags. Each bag has 50 balls in it. There are 30 blue balls in the first bag, 45 blue balls in the second bag, 35 blue balls in the third bag, and 15 blue balls in the fourth bag. Find the probability of selecting a blue ball from one of the four bags at random.
Solution
Total number of bags = 4
Number of bags selected = 1
Probability of selecting a bag = 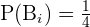
Total number of balls in the first bag = 50
Number of blue balls = 30
Probability of choosing a blue ball from the first bag = 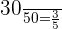
Total number of balls in the second bag = 50
Number of blue balls in the second bag = 45
Probability of choosing a blue ball from the second bag = 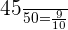
Total number of balls in the third bag = 50
Number of blue balls in the third bag = 35
Probability of choosing a blue ball from the third bag = 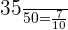
Total number of balls in the fourth bag = 50
Number of blue balls in the fourth bag = 15
Probability of choosing a blue ball from the fourth bag = 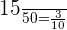
The probability of choosing the blue ball from one of the four bags randomly will be calculated using the total probability rule.
P (blue ball) = 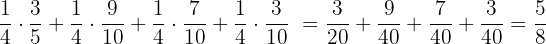
Example 5
Alice wants to go on the trip. The probabilities of going on the trip on a certain day with or without her friend are 0.90 and 0.15 respectively. If the probability that her friend is going on the trip is 0.65, then determine the probability that Alice will go on the trip?
Solution
Suppose A be the event that Alice will go on the trip and B be the event that her friend is is going. We have the following information:
P(B) = 0.65
P(friend not going) = P(B′) = 1 − P(B) = 1 − 0.65 = 0.35
The conditional probabilities of these events will be:
P(A|B) = 0.90
P(A|B') = 0.15
Because the events B and B' form the partitions of the sample space, S, hence, by the total probability theorem, we will calculate the probability like this:
P(A) = P(B) P(A|B) + P(B′) P(A|B′)
= 0.65 x 0.90 + 0.35 x 0.15
=0.585 + 0.0525
= 0.6375
Hence, the probability that Alice will go and her friend is also going on the trip is 0.6375 or 63.75%.













