Chapters

What is Probability Theory?
Probability is the basic building block of many of the tools used in statistics. In order to understand what probability is, it can be helpful to first understand the different branches of statistics and which ones utilize probability.

The picture above shows that under the umbrella of statistics, there are two distinct types of statistics: descriptive and inferential. The table below summarizes the differences between the two as well as the two sub-categories within inferential statistics.
| Descriptive Statistics | Inferential statistics |
| Uses information within the range of the data set to calculate measures of central tendency, spread and to create visualizations | Uses information about the data set to try and make inferences about observations outside the range of the data |
| - | Bayesian statistics assigns probabilities to hypotheses |
| - | Frequentists do not assign probabilities to hypothesis |
As you can see from these distinctions, probability is mostly used in the branch of statistics involved with making predictions, or inferences. Comprehending probability theory from here is quite easy. Probability theory is simply the branch of maths that involves probability.
Random Variable
Random variables can seem like an odd concept when encountered for the first time. This is because we are very familiar with traditional variables in mathematics. Check out the table below to see if you can spot the difference.
| Type | Definition | Example |
| Variable | A symbol representing an unknown value | x = height |
| Random Variable | A variable whose outcome is unknown | Y = toss of a coin |
The biggest difference between traditional variables and random variables is the fact that a random variable’s outcome cannot be known until the process or experiment is run. Notice the difference in notation: random variables are typically depicted by a capital letter. The most classic example of a random variable is a coin toss.

The picture above illustrates four different trials involving a coin toss. As you can see, the outcome of the random variable is not known until the coin is actually flipped in each trial.
Sample Space and Events
Continuing from the example using the coin toss, the next step in understanding probability is knowing what a sample space is. Take a look at the three experiments below, each of which involve a different amount of trials.
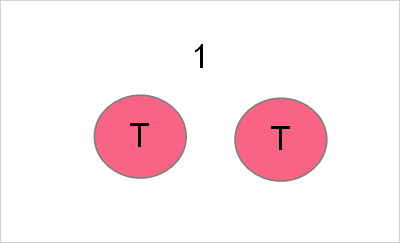
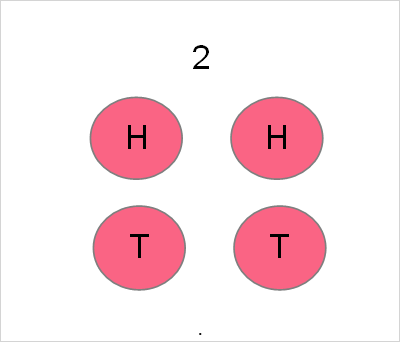

What is something that you notice about this random variable in particular? To be more specific, think about the number of possible outcomes. If you haven’t guessed already, each random variable has what’s called a sample space. The sample space is all possible outcomes for a random variable. The table below shows the sample space for each of the trials in the picture.
| Trial | Results | Sample Space |
| 1 | T,T | S(A) = {H,T} |
| 2 | H,H,T,T | S(A) = {H,T} |
| 3 | H,H,H,T,T,H,T,T | S(A) = {H,T} |
As you can see from the table above, no matter how many trials you run or how many times you flip the coin, the sample space always stays the same. This is because all possible outcomes of the coin toss remain the same: either heads or tails.
Dependent Event
A dependent event in an event whose probability is dependent on another event. In other words, two events are dependent when the outcome of one affects the probability of the other event. Let’s take a look at an example of this. Say that you have the following cards.
| Card Value | Count | Frequency |
| 9 | IIIII II | 7 |
| 6 | II | 2 |
| 4 | III | 3 |
| 3 | I | 1 |
| 1 | II | 2 |
A classic example of a dependent event happens when you choose without replacement. In this example, this means that we would pick a card and not put it back in the deck before we pick the next. Here, we’re interested in the probability of picking a 9.

Originally, there is a 46.7% chance of picking a card with the value of 9. Let’s say that the card you pick is a 4. Now, there are only 14 cards in the deck, which changes the probability of the next card that we pick being a 9.

Independent Event
An independent event, on the other hand, is an event that is not affected by the outcome of another event. Two events can be independent and happen at the same time. While this can seem confusing, take a look at the image below.
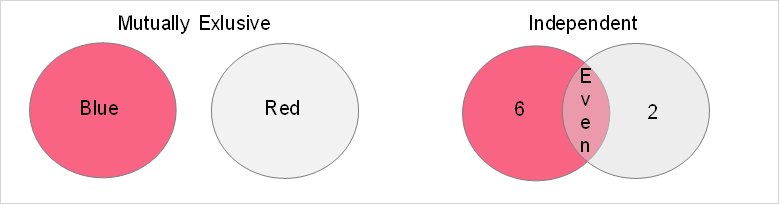
As you can see, an example of an independent event is rolling a dice twice. The first roll is 6 and the second is 2, each having the probability of 1/6 and not affecting each other. These events can occur together when, for example, you're looking for the probability of rolling an even number, which is 3/6.
Mutually exclusive events, on the other hand, are independent events that cannot occur at the same time. Take the example in the image, which shows two events: event A is picking a blue marble and event B is picking a red one. There is no way for these events to occur together.
Multiplication Rule
The multiplication rule in probability deals with the probability of two dependent events happening, which is found by the following formula.

This is the probability of A and B occurring, which is the probability of A multiplied by the probability of B given A. When the events are independent, the formula changes to the following.

Which is simply the probability of A multiplied by the probability of B.
Multiplication Rule Example
In order to understand the multiplication rule, let’s start with an example. Say that there is a jar with bills inside and that you can select one at random. You’re interested in knowing the probability of selecting the highest valued bill given the following frequencies.
| Bank Note | Frequency |
| 5 | 30 |
| 10 | 15 |
| 50 | 2 |
Let’s start with dependent events, which would be selecting a bank note without replacement. You get a chance to select two bills from the jar. The two events here are in the table below.
| Event | Description | Probability |
| A | The probability of selecting a 50 | 2/47 = 0.043 |
| B|A | The probability of selecting a 50 given A has happened. | 1/46 = 0.022 |
| Event | Description | Probability |
| A | The probability of selecting a 50 | 2/47 = 0.043 |
| B | The probability of selecting a 50 | 2/47 = 0.043 |
The probability of selecting both 50s is now 0.043 times 0.043, which is about 0.18%.













