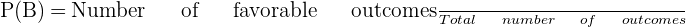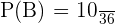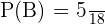Chapters
Probability theory refers to the branch of mathematics that deals with the probability of the events. The probability of a random event measures what is the likelihood of the occurrence of an event. The probability of an event is expressed by a number that lies between 0 and 1. This number is known as a probability measure. The formula for calculating the probability of a random event is given below:
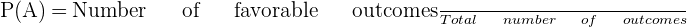
We need probability theory for our daily activities, for instance, analyzing the quantitative data. In this article, we will discuss some of the fundamental concepts or terms related to probability theory and statistics. But before discussing the probability theory and its related concepts, first, let us see what are deterministic experiments, random event, and random variables.

Deterministic Experiments
With deterministic events, we can predict the results of an event before experiment.
Example
For instance, if you throw a ball from the building, the ball will certainly go down. Similarly, if you throw a ball upwards, then it is certain that the ball will go upwards for a certain period of time and then will come back downwards.
Random Experiment
A random experiment refers to a physical situation in which we cannot determine the outcome until it occurs.
It means that with random experiments, we cannot predict the results or outcomes because they depend on chance. Consider the following scenario:
You flip a coin. Can you know before flipping that whether the coin will land on a head or a tail?
The answer is certainly no. Before flipping, you cannot determine the outcome. The same happens when you roll a die. The result cannot be predicted beforehand.
Random Variable
A random variable refers to a variable whose probable set of values are numerical outcomes of a random experiment. A random variable is of two types:
- Discrete random variable: It is a random variable whose set of values can be counted. A discrete random variable has distinct values, for instance, 1,2,3,4,.... Usually, the discrete random variables are whole numbers.
- Continuous random variable: It is a random variable that includes an infinite set of possible values. This type of random variable usually includes measurements.
Probability Theory
A probability theory refers to designating a number to each possible outcome that can occur in a random experiment.
A probability theory involves further concepts or terms which should be studied to understand this theory completely.
Outcome
An outcome refers to each of the possible outcomes of a random experiment. The examples of outcomes include:
- A coin landing on a head when it is flipped
- A die landing on the number 5 when it is rolled.
Sample Space
A sample space refers to the set of all possible results of a random experiment. We denote a sample space by a letter S or by the Greek letter Ω.
For example, if a coin is tossed, the sample space of the coin will be:
S = {H, T}
If a die is rolled, then the sample space of that die will be:
S = {1, 2, 3, 4, 5, 6}
Event
An event refers to the subset of the sample space.
Consider the following example:
Suppose a die is rolled. An event will be an outcome of an odd number, a prime number, or any other.
Example 1
There are blue and red marbles in a bag. Three marbles are drawn from the bag randomly.
- Calculate the sample space
- The probability of drawing three marbles of the same color
- The probability of drawing at least one blue marble
- The probability of drawing exactly one red marble
Solution
1. The sample space means to write all possible outcomes of a random experiment. The sample space of the above experiment is:
S = {(b,b,b); (b,b,r); (b,r,b); (r,b,b); (b,r,r); (r,b,r); (r,r ,b); (r, r,r)}
2. Now, we will calculate the probability of drawing three marbles of the same color.
The probability of drawing three marbles of the same color are (b,b,b) and (r,r,r). Use the following formula to calculate the probability:
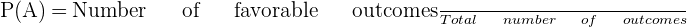
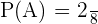

3. In this part, we will compute the probability of drawing at least one blue marble. To do so, we will list down all possible outcomes from the sample space:
B= {(b,b,b); (b,b,r); (b,r,b); (r,b,b); (b,r,r); (r,b,r); (r,r ,b)}
We will use the following formula to calculate the probability:
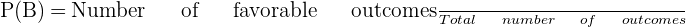
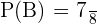
4. The probability that exactly one marble is red will be calculated by determining the number of possible events in which an exactly one marble is red and dividing it by the total number of possible events:
C = {(b,b,r); (b,r,b); (r,b,b)}

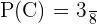
Example 2
Two dice are rolled simultaneously. Calculate:
1. The sample space
2. The probability that two dice land on the same number
3. the probability that the both dice land on an even number
Solution
1. The sample space refers to the list of all possible outcomes of a random experiment. The sample space of the two dice will be:
Sample space = S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2), (4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
Hence, the total number of all possible outcomes is 36.
2. Now, we will calculate the probability of two dice landing on the same number. First, we will see the number of possible outcomes when two dice land on the same number:
P(A) = (1,1), (2,2), (3,3), (4,4), (5,5), (6,6)
Hence, the number of possible outcomes is 6.
We will use the following formula to calculate the probability:
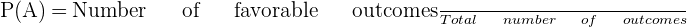
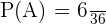

3. In this step, we will compute the probability of both the dice landing on an even number. For this, first, we will calculate the list of possible outcomes when both the dice land on an even number.
P(B) = (2,2), (4,4), (6,6), (2,4), (2,6), (4,2), (4,4), (4,6), (6,2), (6,4)
Hence, the total number of favorable outcomes is 10. We will use the following formula to compute the probability of both the dice landing on an even number.