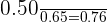In this article, we will solve some examples related to probability. So, let us get started.

Example 1
Solution



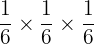
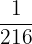



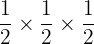

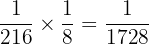
Example 2
Find the probability of selecting three composite number cards from the deck of 52 cards.
Solution
First, we will se how a deck of 52 cards is distributed. In a deck of 52 cards, we have:
- Four suits (Each suite has 13 cards)
- Two suits black and two are red
- The cards in each suit include a king, a queen, a jack, an ace, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
In each suit, there are 5 composite numbers 4, 6, 8, 9, and 10. Hence, in four suits, there are 20 composite numbers.
Number of composite number cards in a deck = 20
Total number of cards in a deck = 52
The probability of selecting a composite number card from a deck = 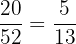
In the second step, we will find the probability of picking up the second composite number card from the deck.
Number of composite number cards left in a deck = 20 - 1 = 19
Total number of cards left in a deck = 51
The probability of selecting a composite number card, given a composite number card has already been drawn = 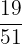
In the third step, we will calculate the probability of selecting the third composite number card from the deck.
Number of composite number cards left in the deck = 19 - 1 = 18
Total number of cards left in a deck = 51 - 1 = 50
Probability of selecting the third composite number card from the deck = 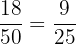
In this problem, we have to calculate the probability of selecting three composite number cards from a deck of 52 cards. Hence, we will multiply all the probabilities together like this:
P (3 composite numbered cards) = 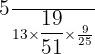
=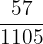
Example 3
In a class of 25 students, there are 15 girls and 10 boys. 7 of the 15 girls and 3 of the 10 boys can speak German. If a students is selected randomly, find the probability that the selected student:
a) can speak German
b) Is a girl or a boy who speaks German
Solution
Part a
Number of girls who can speak German = 7
Number of boys who can speak German = 3
Total number of students in the class = 25
Probability of randomly selected student speaking the German = 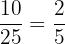
Part b
Number of boys who speak German = 3
Total number of students in the class = 30
Probability of selecting a boy who speaks German = 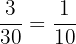
Number of girls who speak German = 7
Total number of students in the class = 30
Probability of selecting a girl who speaks German = 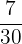
The probability of selecting a girl or a boy who speak German = 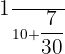
= 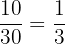
Example 4
Sam accidentally mixes eight functional and four fuse bulbs. To find the defective bulbs, he tests each bulb one by one, without replacement. What is the probability that he finds the defective bulbs in the first three experiments?
Solution
Suppose 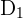 ,
,  , and
, and  are the events that he finds the fuse bulbs.
are the events that he finds the fuse bulbs.
The probability of selecting the first fuse bulb = 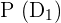 =
= 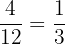
The probability of selecting the second fuse bulb given the first one was also fuse = 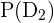 =
= 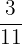
The probability of selecting the third fuse bulb, given that the first two bulbs were also fuse = 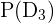 =
= 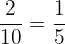
The probability of finding the fuse bulbs in the first three experiments = 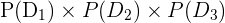 =
= 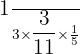
= 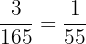
Example 5
Factory workers produce products that are either excellent (77%), slightly defective (13%), or completely defective (10%). All the parts undergo routine inspection. Out of the produced products, the completely defective products are discarded. What is the probability that a product is excellent given that it has passed the inspection?
Solution
Let E, S.D and C.D be the events that a randomly chosen product is excellent, slightly defective and completely defective respectively.
Probability of selecting an excellent product = P(E) = 0.77
Probability of selecting a slightly defective product = P(S.D) = 0.13
Probability of selecting a completely defective product = P(C.D) = 0.10
We have to compute the probability that a product is excellent, given that it has passed the routine inspection.
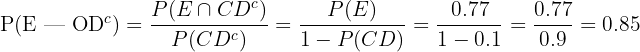
Example 6
A coin is thrown four times. What is the probability that at least one tail is obtained?
Solution
Total number of trials = 4
Total number of possible outcomes = 2 x 2 x 2 x 2 = 16
We can get head all the four times when tossing the coin. Except this, every possible outcome can have at least one tail. Hence, the number of possible outcomes in which there can be at least one tail is 15.
Probability of getting (at least) 1 tail = 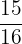
Example 7
In a class, 65% of the students passed math exam, 20% passed science exam and 50% passed both math and science exam. Suppose a student is chosen randomly. If he/she has passed a math exam, what is the probability that he/she has also passed the science exam?
Solution
Probability of passing a math exam = P(M) = 0.65
Probability of passing a science exam = P(S) = 0.20
Probability of passing both math and science exam =  = 0.50
= 0.50
P (Science|Math) = 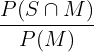
=