Chapters

What is the z table?
The standard Normal z-table is also known as the z-table. We employ the standard normal table to test the hypothesis. This hypothesis also includes the tests on the difference between two means and proportions. In a standard normal distribution, a z-table allows us to determine the percentage of values below a z-score. The z-score or standard score depicts the number of standard deviations a value in the data is above or below the mean.
The Purpose of Using Z-table
We come across data that contains a different set of values. For instance, the ages of the people might range from 15 to 85 and the weight may range from 5 pounds to 350 pounds. These ranges of the data sets are extremely wide which makes it difficult for a person to analyze the data set. Hence, to facilitate the analysis of the data, we standardize the normal curve in such a way that the mean of the data set is zero and its standard deviation is one. After we have standardized the curve, we use a Z table to find the percentages under the curve. The bell curve of normal distribution is given below:
Remember that the z-table only tells the less than values. To determine the greater than values, we need to subtract the less than value from the z-table and then subtract it from 1.
Z-score formula
The formula for calculating a z-score is given below:
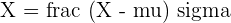
Here:
x = a test value from the data
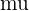 = mean of the data set
= mean of the data set
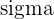 = Standard deviation of the data set
= Standard deviation of the data set
Interpreting the Z-score
We can interpret the z-score in the following ways:
- If a z-score is less than 0, then it means that the test value is less than mean
- If a z-score is greater than 0, then it means that the test value is greater than mean
- If a z-score is equal to 0, then it reflects that the test value is equal to the mean
- If a z-score is equal to 2, then it reflects that a test value is 1 standard deviation greater than the mean. Similarly, a z-score of 2 signifies a test value that is 2 standard deviations greater than the mean, and so on.
- If a z-score is equal to -1, then it means that the test value is 1 standard deviation less than the mean. Similarly, a z-score of -2 represents a test value that is 2 standard deviations less than the mean and so on.
- In a large data set, approximately 68% of the values have a z-score between -1 and 1, 95% have a z-score between -2 and 2, and almost 99% of values have a z-score between -3 and 3.
In the next section, we will see how to find the values from the z-table through examples.
Example 1
Find 
Solution
To find the probability using the Z-table, first, locate where the row for 1.7 overlaps with the column 0.0. This value in the Z-table is 0.9554. Remember that the Z-table only gives less than probabilities. In this question, the probability has less than symbol, so 0.9554 is the final answer. The graph of this distribution is given below:
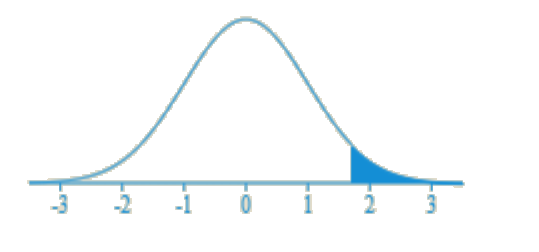
Example 2
Find 
Solution
We will follow the same steps as in the previous examples to find the z-value from the table. However, after we will locate the value from the table, we will subtract it from 1 to get the value that is greater than equal to 1.7. This is because the z-table only gives us less than probabilities. The value from the z-table located in the 1.7 row and the corresponding 0.0 column is 0.9554.


The bell-shaped curve for this distribution is given below:
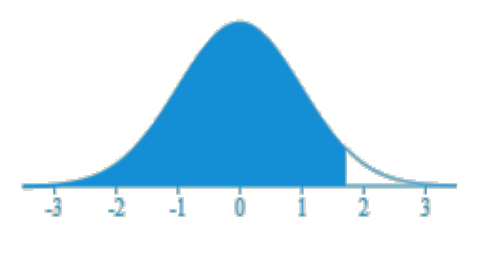
Example 3
Find 
Solution
In this question, the value of Z is between two values. In cases where the value of Z is between two values, we find the probabilities of each value and subtract the values. In this question, first, we will use the z-table to find the probability where the row -0.7 overlaps the column 0.00. In this case, the value is 0.2420.
In the next step, we will use the z-table again to find the value that is present in the intersection of row 2.0 and column 0.00. This value is 0.9772.
Since the z-table only shows us the less than probabilities, hence we can write the probabilities like this:
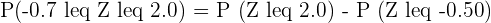

= 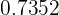
The graph of this probability distribution is given below:
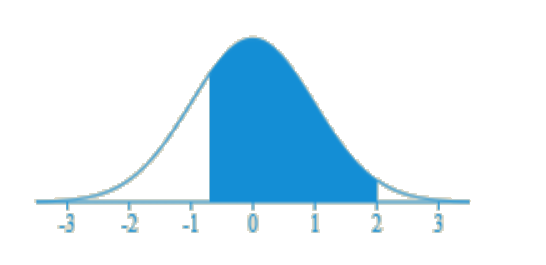
Example 4
Find 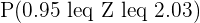
Solution
In this question, the value of Z is between two values. In cases where the value of Z is between two values, we find the probabilities of each value and subtract the values. In this question, first, we will use the z-table to find the probability where the row0.9 overlaps the column 0.05. In this case, the value is 0.8289.
In the next step, we will use the z-table again to find the value that is present in the intersection of row 2.0 and column 0.03. This value is 0.9788.
Since the z-table only shows us the less than probabilities, hence we can write the probabilities like this:

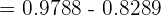
= 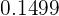
The graph of this probability is given below:

Example 5
The mean score of the students in math exam is 85 with a standard deviation of 10. What is the probable percentage of students who scored more than 90 in the math exam?
Solution
The z-score will be calculated using the following formula:
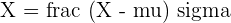
Here, X = 90

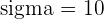
Substitute these values in the z-score formula like this:
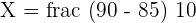
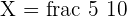
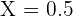
Now, we will use the z-table to determine the probability that is located at the intersection of the row 0.5 and column 0.00. This probability is 0.6915.
It means that 69.15% of the students obtained the core within 90. Hence, the percentage of students who scored more than 90 is:
= 100% - 69.15% = 30.85%
Example 6
The mean weight of athletes is 198 pounds with a standard deviation of 15. What is the probable percentage of athletes who weigh more than 220 pounds?
Solution
Here,
The mean weight of athletes = 198 pounds
Standard deviation = 15
The test value = X = 220
Substitute these values in the formula for calculating the z-score below:
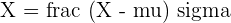
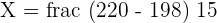
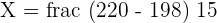
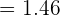
Now, we will use the z-table to determine the probability value that lies at the intersection of row 1.4 and column 0.06. This value is 0.9279. Since we have to tell the probable weight of athletes that is greater than 220 pounds, so we will subtract 0.9279 from 1 and convert the remainder into a percentage like this:
= 1 - 0.9279 = 0.0721
= 7.21%
Hence, there is 7.21% of the athletes may weigh more than 220 pounds.













