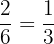Chapters
In this article, we will discuss how to solve problems related to probability. But before proceeding to solve the problems, first, let us see what is a probability.
In mathematics, probability refers to the possibility of the occurrence of a random event. The value of probability ranges from 0 to 1 and it is never expressed as a negative number. It is a branch of mathematics that deals with the forecast of the events. To calculate the probability of a random event, you must know the total number of outcomes.

Why we use Probability?
We cannot predict many events with total certainty. For example, we cannot say that it will certainly rain tomorrow. Instead, we can say that there is a 90% chance that it will rain tomorrow. As you have seen that we have predicted the rain in percentage. This is because we can convert the probability into a percentage by multiplying it by 100%. In terms of probability, we can say that the probability that it will rain tomorrow is 0.9. If there is a 100% chance that an event will occur, then the probability of such an event is 1. The probability of an impossible event is 0.
Probability Formula
The formula to calculate the probability of an event is given below:

In the next section, we will solve some examples related to probability.
Example 1
The probability of John attending an event is 0.7. What is the probability that he will not attend the event?
Solution
The probability of attending an event = 0.7
The probability of not attending an event = 1 - 0.7 = 0.3
Example 2
There are 12 balls in a bag. Out of 12 balls, 3 are red, 4 are blue, and 5 are green. What is the probability of picking up:
a) a red ball
b) a red or green ball
c) a red and blue ball
Solution
There are three parts of this problem. We will solve each part step by step.
Part a
Number of red balls in a bag = 3
Total number of balls in a bag = 12
Probability of picking up a red ball = 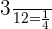
Part b
Number of red balls in a bag = 3
Number of green balls in a bag = 5
Total number of balls in a bag = 12
Probability of picking up a red ball = P(R) = 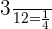
Probability of picking up a green ball = P(G) = 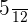
Probability of picking up a red or green ball = P(R) U P(G)
= 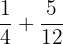
= 
Part c
Probability of picking up a red ball = P(R) = 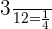
Probability of picking up a blue ball = P(B) = 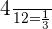
Probability of picking up a red and blue ball = 0
We cannot pick up both the balls at the same time. So, both the events are mutually exclusive. The probability of mutually exclusive events is always zero.
Example 3
From a deck of 52 cards, what is the probability of picking up a queen or jack card?
Solution
Total number of cards in a deck = 52
Number of queen cards= 4
Probability of picking up a queen card = P(Q) = 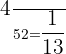
Number of jack cards = 4
The probability of picking up a jack card = P(J) = 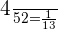
The probability of picking up a queen or a jack card = P(Q) U P(J)
=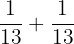
=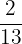
Example 4
A box contains 5 red, 8 green, 12 blue, and 10 yellow marbles. If three marbles are drawn from the box at random, what is the probability that the first marble will be red, second will be yellow, and third will be green?
Solution
Total number of marbles in a box = 5 + 8 + 12 + 10 = 35
Number of red marbles = 5
Probability of picking up a red marble first = P(R) = 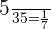
Number of marbles left = 35 - 1 = 34
Number of yellow marbles in a box = 10
Probability of picking up a second yellow marble = P(Y) = 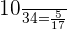
Number of marbles left = 34 - 1 = 33
Number of green marbles = 8
Probability of picking up a third green marble = P(G) = 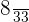
Example 5
Two dice are rolled simultaneously. What is the probability that the sum is:
a) equal to 5
b) less than 5
c) greater than 5
Solution
Part a
Total number of outcomes = 6 x 6 = 36
Sample space = S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2), (4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }
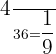
Part b
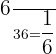
Part c
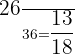
Example 6
Solution
Part a
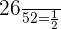
Part b
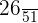
Example 7
Solution



Example 8
Solution


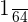
Example 9
Solution
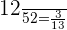
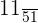
Example 10
Solution