In this article, we will find solved problems related to probability.

Example 1
A bag has 10 red balls, 5 yellow balls, and 15 green balls. If a ball is selected randomly, then calculate the probability that it will be:
a) Red
b) Yellow
c) Green
d) Not red
e) Not green
f) Two red balls
g) Two green balls
Solution
Part a
Total number of balls in the bag = 10 + 5 + 15 = 30
Number of red balls in the bag = 10
Probability of picking up a red ball = 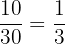
Part b
Number of yellow balls in the bag = 5
Probability of picking up a yellow ball = 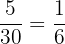
Part c
Number of green balls in the bag = 15
Probability of picking up a green ball = 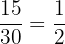
Part d
Probability of picking up a red ball = 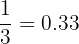
Probability of not picking up a red ball = 1 - 0.33 = 0.67
Part e
Probability of picking up a green ball = 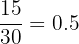
Probability of not picking up a green ball = 1 - 0.5 = 0.5
Part f
Probability of picking up the first red ball = 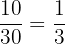
Probability of picking up the second red ball = 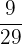
Probability of picking up two red balls = 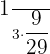
=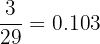
Part g
Probability of picking up the first green ball = 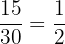
Probability of picking up the second green ball = 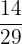
Probability of picking up two green balls = 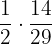
= 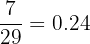
Example 2
There are five bags.
- Bag 1 has 30 balls in it, out of which 6 are red
- Bag 2 has 25 balls in it, out of which 5 are red
- Bag 3 has 27 balls in it, out of which 8 are red
- Bag 4 has 15 balls in it, out of which 7 are red
- Bag 5 has 40 balls in it, out of which 8 are red
Find the probability of selecting a red ball from one of the five bags at random.
Solution
Total number of bags = 5
Number of bags selected = 1
Probability of selecting a bag = 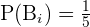
Total number of balls in the first bag = 30
Number of red balls = 6
Probability of choosing a red ball from the first bag = 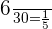
Total number of balls in the second bag = 25
Number of red balls in the second bag = 5
Probability of choosing a red ball from the second bag = 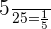
Total number of balls in the third bag = 27
Number of red balls in the third bag = 8
Probability of choosing a red ball from the third bag = 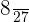
Total number of balls in the fourth bag = 15
Number of red balls in the fourth bag = 7
Probability of choosing a red ball from the fourth bag = 
Total number of balls in the fifth bag = 40
Number of red balls in the fifth bag = 8
Probability of choosing a red ball from the fifth bag = 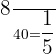
The probability of selecting the red ball from one of the five bags randomly will be calculated using the total probability rule.
P (red ball) = 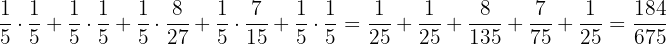
Example 3
Two dice are rolled simultaneously. Calculate:
a) The probability of two dice landing on the odd numbers
b) The probability that the sum of the numbers on two dice is an even number
c) The probability that the difference of the numbers on two dice is equal to zero
Solution
First, we will calculate the sample space. The sample space is the list of all possible outcomes of a random experiment. The sample space of the two dice is given below:
Sample space = S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2), (4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
This shows that the total number of possible outcomes is 36.
Part a
Here, we will compute the probability that two dice land on the odd numbers. To calculate this probability, first, let us see the number of possible outcomes when two dice land on the odd numbers:
{(1,1),(1,3),(1,5), (3,1), (3,3), (3,5), (5,1),(5,3),(5,5)}
Number of possible outcomes = 9
Total number of possible outcomes = 36
Probability of two dice landing on the odd numbers = 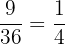
Part b
To calculate the probability that the sum of the numbers on two dice is an even number, first, we will see the number of possible outcomes.
{(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(4,6), (5,1),(5,3),(5,5), (6,2),(6,4),(6,6)}
Number of possible outcomes = 18
Total number of possible outcomes = 36
Probability that the sum of the numbers on two dice is an even number = 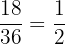
Part c
Now, we will calculate the probability that the difference of the numbers on two dice is equal to zero. For this, first, we should find the number of possible outcomes in which the difference of numbers on two dice is equal to zero.
{ (1,1),(2,2),(3,3),(4,4),(5,5),(6,6)}
Number of possible outcomes = 6
Total number of possible outcomes = 36
Probability of having the difference of two numbers on the dice equal to zero = 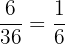
Example 4
A die and a coin are thrown simultaneously. What is the probability of getting an odd number on the dice and tail on the coin?
Solution
Total number of possible outcomes on a die = 6
Total number of odd numbers on the die = 3
Probability of getting an odd number on the die = 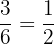
Total number of possible outcomes on a coin = 2
Probability of getting a tail on the coin = 
The probability of getting an odd number on the die and tail on the coin = 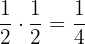
Example 5
Three coins are tossed simultaneously. What is the probability of getting heads on all the three coins?
Solution
Probability of getting a head on the first coin = 
Probability of getting a head on the second coin = 
Probability of getting a head on the third coin = 
Probability of getting heads on all the three coins = 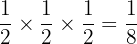
Example 6
Two dice are rolled simultaneously. What is the probability of getting 2 or 6 on both the dice?
Solution
Probability of getting 2 or 6 on the first dice = 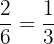
Probability of getting 2 or 6 on the second dice = 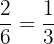
Probability of getting 2 or 6 on both the dice = 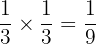
Example 7
Two workers are working in a house. The probabilities of completing the work on time with and without rain are 0.70 and 0.25 respectively. If the probability of rain on a certain day is 0.35, then determine the probability that the workers will complete the work on time?
Solution
Suppose A be the event that workers will complete the work on time and B be the event that it is going to rain. We have the following data:
P(B) = 0.35
P(not raining) = P(B′) = 1 − P(B) = 1 − 0.35 = 0.75
The conditional probabilities of these events will be:
P(A|B) = 0.70
P(A|B') = 0.25
We will use the total probability rule to calculate the probability like this:
P(A) = P(B) P(A|B) + P(B′) P(A|B′)
= 0.35 x 0.70 + 0.75 x 0.25
= 0.4325













