Chapters
In statistics, the median of a data set represents the value that separates the higher half of the data set from the lower half. We can calculate the median of a sample, population, or probability distribution. In general, we can say that the median is the middle value of the data set. The primary attribute of the median is that unlike the mean it is not skewed by extremely small or large values of the data set. Hence, it better represents the middle value of the data set. For instance, if we had to compute the average income of people living in a specific area, then the median income will better represent the typical income instead of the mean. This is because the income distribution can be extremely skewed because some people can be earning very less and some may be earning a lot higher than average. The median breaks down the 50% statistic. That is why it is of great importance in robust statistics. The median does not give a result that is extremely large or extremely small, hence it is a reliable statistic. We can define median formally as:
The median of the data set segregates the upper half of the distribution from the lower half
In other words, we can say that the median of the data set divides it into two equal parts. We denote the median as Me.
We can compute the median only for quantitative variables. In the next section, we will see how to calculate the median of the data set.

Calculation of the Median
Follow these steps to calculate the median of the data set.
Step 1
Arrange the data in ascending (from smallest to largest value) or descending order (from largest to smallest value).
Step 2
Two important things should be considered in this step.
- A series with an odd number of elements: If the series has an odd number of elements, then the median is the middle number. For instance, if the data set has 7 elements, then the median of the data set will be the fourth number.
- A series with an even number of elements: If the series has an even number of elements, then the median is the average of the middle two numbers. For instance, if the data set has 10 elements, then the median of the data set will the average of 5th and 6th numbers.
Examples
1. Calculate the median of the following data set:
7, 9, 10, 4, 3, 2, 1, 8, 12
First, we will arrange the above data set in ascending order like this:
1, 2, 3, 4, 7, 8, 9, 10, 12
Now, we will count the number of terms and will see whether the data set has an odd or even number of elements. The total number of elements in the above data set is 9. It means that the data set has an odd number of elements. Hence, the median will be the 5th number. The fifth number in the above data set is 7. Hence, the median of the above data set is 7.
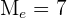
You can see that the number 7 has divided the series into two halves. It means that the series has 4 numbers before the median and four numbers after it.
12, 10, 7, 14, 15, 17, 18, 22
First, we will arrange the above data set in ascending order like this:
7, 10, 12, 14, 15, 17, 18, 22
Now, we will count the number of terms and will see whether the data set has an odd or even number of elements. The total number of elements in the above data set is 8. It means that the data set has an even number of elements. Hence, the median will be the average of the middle two numbers. The middle two numbers are the numbers at 4th and 5th positions. These numbers 14 and 15 divide the data into two halves. Hence, the median will be the average of 14 and 15:

Median of the Grouped Data
| Age | Number of children | Cumulative frequency |
|---|---|---|
| 0-3 | 12 | 12 |
| 3-6 | 10 | 22 |
| 6-9 | 9 | 31 |
| 9-12 | 10 | 41 |
| 12-15 | 4 | 45 |
Calculate the median age of the children in that street from the above grouped data.
Formula for Calculating the Median of a Grouped Data
The formula for calculating the median from a grouped data is given below:
Median = 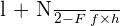
Here:
l reflects the lower limit or class boundary of the median class
F reflects the cumulative frequency of the class before the median class
f represents the frequency of the median class
N represents the total number of observations
h reflects the width of the median class
First, let us calculate the total number of observations from the above data. The total number of observations are 12 + 11 + 8 + 10 + 4 = 45.
Hence, we can say that N = 45.
Now, let us see what is the median class. It is not possible to find the median by simply observing the data. Hence, we will divide the total number of observations by 2 to get the idea of the median class like this:
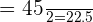
Now, we will see the table to see when the total number of children becomes greater than 22.5. It is class 6 - 9 when the number of children becomes greater than 22.5. Hence, we can say that it is the median class.
Now, that we have located the median class, we can easily find out the other unknowns.
F is the cumulative frequency before the median class which is 22.
f represents the frequency of the median class. The frequency of the median class is 9.
the lower limit of the median class 6-9 is 6 which represents l.
The width of the median class is represented by h. The width is calculated by taking a difference of the upper and lower limit of the class. The median class 6-9 has a width of 3.
Now, we will substitute all the above values in the formula below to get the median:
Median = 
Median = 
Median = 
Median = 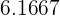
Hence, the median age of the children living in that street is approximately 6.













