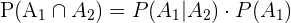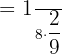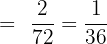Chapters

Exercise 1
Two balls are drawn from a box that contains three blue, four red, one green and one yellow ball. What is the probability of selecting:
1 The first red ball
2 The second blue ball without replacement
Exercise 2
A box has 8 red balls, 5 yellow and 7 green. If a ball is extracted at random, calculate the probability that it will be:
1 Red
2 Green
3 Yellow
4 Not red
5 Not yellow
Exercise 3
Two dice are thrown into the air simultaneously. Calculate:
- The probability that the sum of the dice will total 7.
- The probability that the sum of the dice will be an even number.
- The probability that the sum of the dice will be a multiple of three.
Exercise 4
Three dice are thrown simultaneously. Calculate the probability of:
- Obtaining a six in all three die.
- Obtaining the same numbers on all the three dice
Exercise 5
- An even number
- A multiple of three
- A five or a six
Exercise 6
A worker at the factory accidentally mixes seven good and two defective lamps. To find the defective lamps, he tests each lamp one by one, randomly without replacement. What is the probability that he is lucky and find both the defective lamps in the first two attempts?
Solution of Exercise 1
Total number of balls in a bag = 9
Probability of selecting the first red ball = P(A) = 
Probability of selecting the second blue ball = P(B) = 
Solution of Exercise 2
Probability of selecting a red ball = P(A) = 
Probability of selecting a green ball = P(B) = 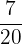
Probability of selecting a yellow ball = P(C) = 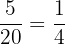
Probability of selecting a ball that is not red = P(D) = 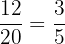
Probability of selecting a ball that is not yellow = P(E) = 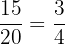
Solution of Exercise 3
Total number of outcomes of two dice = 36
Sample space = S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2), (4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
Number of events in which the total sum of the numbers on the dice will be 7 = (1,6), (2,5), (3,4), (4,3), (5,2), (6,1)
Probability of getting the sum 7 on two dice = 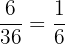
Number of events in which the sum of the numbers on the dice is multiple of 3 = (1,2), (1,5), (2,1), (2,4), (3,3), (3,6), (4,2), (4,5), (5,1), (5,4), (6,3), (6,6)
Probability of getting a sum that is multiple of 3 = 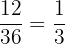
Solution of Exercise 4
Total number of outcomes of three dice = 6 x 6 x 6 = 216
Probability of obtaining 6 on all the three dice = 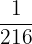
Probability of obtaining the same numbers on all the three dice = 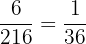
Solution of Exercise 5
Probability of getting an even number on a die = 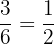
Probability of getting a multiple of 3 on a die = 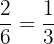
Probability of getting a five or a six = 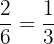
Solution of Exercise 6
Suppose 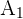 and
and 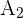 are the events that he finds the defective lamps.
are the events that he finds the defective lamps.
The probability of selecting the first defective lamp =  =
= 
The probability that the second lamp is also defective given the first one is defective = 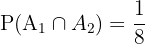
We know that we have to find the probability that both the lamps are defective. We will use the following formula of conditional probability:
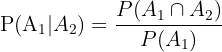
We have to find only  because we already have
because we already have  .
.