Chapters
Points, planes, and lines are undefined terms that act as a starting point for geometry and plane geometry. In this article, we will discuss points, their properties, and the method of calculating distance between them in detail.

What is a Point?
A point is a dot that has zero length, width, or height. It describes the exact location and is zero-dimensional. Zero-dimensional means that a point has absolutely no dimension. Consider the following figure which shows the points A, B, C, and D.

You can see that the points are denoted by the capital letters A, B, C and D. In the next section, we will discuss some of the properties of points in detail.
Properties of Points
The properties of points are discussed below:
1. There are infinite elements called points.
2. A line is made up of infinite points. Consider the figure below in which the line segment AB is composed of many points.
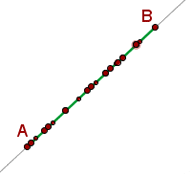
3. Between two points of a straight line infinite points are comprised.
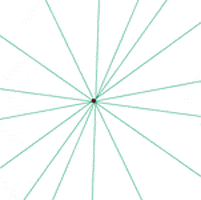
4. Infinite straight lines pass through a point on the plane.
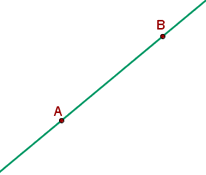
5. Two points determine a line.

6. Three non-linear points indicate a plane
Distance Between Two Points
Distance between two points refers to the length of the line segment that joins the two given points. Hence, we can calculate the distance between two lines in a coordinate plane by finding the length of the line segment that is formed by connecting those two points. In coordinate geometry, we have a specific formula that we can use to calculate the distance between two points. The formulas for computing the distance between two points in two-dimensional and three-dimensional planes are given below.
Formula for Finding the Distance in a Two Dimensional Plane

Here,  and
and 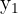 represent the coordinates of the first point and
represent the coordinates of the first point and  and
and 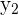 depict the coordinates of the second point. The above formula is used to compute the distance between two points in the two-dimensional plane only. For calculating the distance between two points in a three-dimensional plane, we have a slightly different formula which is given below.
depict the coordinates of the second point. The above formula is used to compute the distance between two points in the two-dimensional plane only. For calculating the distance between two points in a three-dimensional plane, we have a slightly different formula which is given below.
Formula for Finding the Distance in a Three-Dimensional Plane
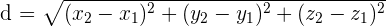
Here,  ,
, 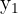 , and
, and 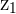 represent coordinates of the first point and
represent coordinates of the first point and  ,
, 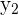 , and
, and  depict the coordinates of the second point.
depict the coordinates of the second point.
In the next section, we will solve a couple of examples in which we will calculate the distance between two points in a plane.
Example 1
Find the distance between the points P (3, 4) and Q (8, 2).
Solution
According to this example, the coordinates of first and second points are as follows:
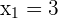
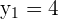
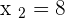
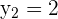
The formula for calculating the distance between two points is given below:

Now, we will substitute these points in the above formula to get the distance between two points P and Q:
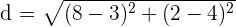
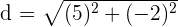
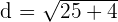

Hence, the distance between two points P and Q is  which is equal to 5.28 in decimal form.
which is equal to 5.28 in decimal form.
Example 2
Find the distance between points A (-5, 1) and B (6, -3).
Solution
According to this example, the coordinates of first and second points are as follows:
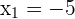

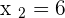

The formula for calculating the distance between two points is given below:

Now, we will substitute these points in the above formula to get the distance between two points A and B:
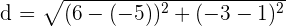



Hence, the distance between two points A and b is 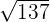 which is equal to 11.74 in decimal form.
which is equal to 11.74 in decimal form.
Example 3
Find the value of "a" if the distance between the points M (5, 8) and N (1, a) is 5 units.
Solution
According to this example, the coordinates of first and second points are as follows:

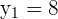
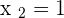

The formula for calculating the distance between two points is given below:

Now, we will substitute these points in the above formula to get the distance between two points M and N:
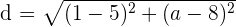
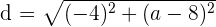
Now, substitute d = 5 in the above expression because the distance is already given and we just have to find the second coordinate of the point N:
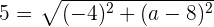
Now, we will square both sides of the above equation to get the following expression:
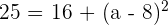

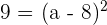
Now, we will take the square root of both sides of the expression like this:

Now, we have two expressions. Either a - 8 = +3 or a - 8 = -3. Each of the two expressions will be evaluated separately like this:
a - 8 = +3
a = +3 + 8 = 11
For a - 8 = -3:
a - 8 = -3
a = - 3 + 8
a = 5
Hence, the value of a is either 5 or 11. For both the values the distance between the points will be equal to 5.
Example 4
Find the value of m if the distance between the points A (-2, m) and N (6, 1) is 10 units.
Solution
According to this example, the coordinates of first and second points are as follows:
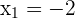
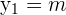
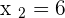

The formula for calculating the distance between two points is given below:

Now, we will substitute these points in the above formula to get the distance between two points A and B:
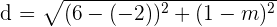
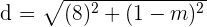
Now, substitute d = 10 in the above expression because the distance is already given and we just have to find the second coordinate of the first point A:
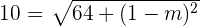
Now, we will square both sides of the above equation to get the following expression:

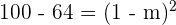
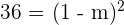
Now, we will take the square root of both sides of the expression like this:

Now, we have two expressions. Either 1 - m = +6, or 1 - m = -6. We will evaluate each of these expressions separately as shown below:
1 - m = +6
1 - 6 = m
m = -5
For 1 - m = -6:
1 - m = -6
m = 1 + 6
m = 7
Hence, the value of m is either - 5 or 7. For both the values the distance between the points will be equal to 10 units.
Example 5
Find the distance between the points A (1, 5, 6) and B (8, 2, 4) in a three-dimensional plane.
Solution
According to this example, the coordinates of first and second points are as follows:
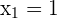
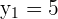
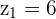
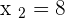
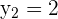
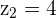
The formula for calculating the distance between two points in a three dimensional plane is given below:
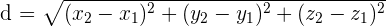
Now, we will substitute these points in the above formula to get the distance between two points A and B:
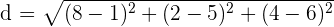
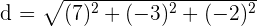
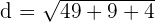

Hence, the distance between two points A and B is  which is equal to 7.87 units in decimal form.
which is equal to 7.87 units in decimal form.
Summarise with AI:












Hi Emma nice to meet u I love reading and solving mathematics problem