
Introduction
In geometry, shapes often work together. When we draw a polygon inside a circle such that every vertex (corner) touches the circumference of the circle, we call it an inscribed polygon. The circle surrounding it is called the circumcircle. These shapes are also known as cyclic polygons.
While any polygon can be inscribed in a circle if its vertices line up correctly, regular polygons (where all sides and angles are equal) are the most common examples we study. For regular polygons, the centre of the polygon is exactly the same as the centre of the circle.
Think of the word inscribed as a "perfect fit" where one geometric shape is tucked neatly inside another. In geometry, it specifically means that one figure is drawn inside another so that they touch at as many points as possible without crossing over any sides.
Key Theory and Formulas
When a regular polygon is inscribed in a circle with radius r, there are specific mathematical relationships between the radius, the side length, and the apothem (the distance from the centre to the midpoint of a side).
1. Inscribed Square
Imagine a square inside a circle. If you draw lines from the centre to two adjacent corners, you form a right-angled triangle.
- The two legs of the triangle are the radius (r).
- The hypotenuse is the side length (l) of the square.
Using Pythagoras' Theorem:
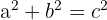
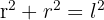
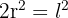
Taking the square root gives us the formula for the side length:
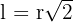
2. Inscribed Regular Hexagon
A regular hexagon is unique because it can be divided into 6 equilateral triangles meeting at the centre.
- This means the side length (l) is exactly equal to the radius (r).
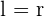
The Apothem (a):
The apothem is the height of one of these equilateral triangles. Using Pythagoras on half of the triangle:
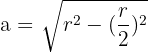
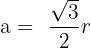
3. Inscribed Equilateral Triangle
For an equilateral triangle inscribed in a circle, the relationship between the side length (s) and the radius (r) is derived using trigonometry (specifically the sine rule or 30-60-90 triangles).
The formula is:
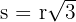

Practice Questions & Solutions
Find the side length of a square inscribed in a circle with a radius of 5 cm. Give your answer to 2 decimal places.
We know the relationship between the side (l) and radius (r) for a square is derived from Pythagoras.
Formula:
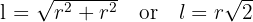
Substitute r = 5:

Calculate the value:
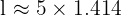
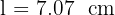
Calculate the apothem of a regular hexagon inscribed in a circle with a radius of 4 cm.
First, remember that for a hexagon, the side length equals the radius.
Side length = 4 cm
The apothem forms a right-angled triangle with the radius and half the side length.
Hypotenuse = Radius = 4
Base = Half of side = 2
Height = Apothem (a)
Using Pythagoras:
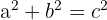

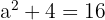
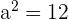
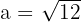
Simplify the surd:
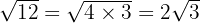
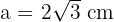
(Or approx 3.46 cm).
An equilateral triangle is inscribed within a circle. The area of the circle is 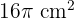 .
.
Find the length of the side of the triangle.
We are given the area of the circle:
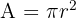
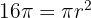
Divide by 
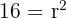
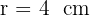
Step 2: Calculate the side length.
Now we use the formula for an inscribed equilateral triangle:
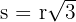
Substitute r = 4:
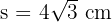
(Or approx 6.93 cm).
Summarise with AI:












Hi Emma nice to meet u I love reading and solving mathematics problem