Chapters
In this article, we will discuss what is parallelogram, its different types, angles and properties. You will also learn how to calculate the area and perimeter of a parallelogram. First, we will start with the introduction of parallelograms.

Introduction
A parallelogram refers to a two dimensional geometrical figure, whose opposite sides are parallel to each other.
It is in fact a type of polygon (a figure with multiples sides) in which the length of the parallel sides is the same. The opposite angles of the parallelogram are also of the same measure. It is also known as a quadrilateral whose parallel sides exist in pairs. If the length if the parallel sides of a geometric figure is not the same, then we cannot call it a parallelogram. Similarly, if the opposite interior angles of a figure are not congruent, then the figure is not a parallelogram. All the interior angles of a parallelogram must add up to 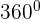 .
.
In the next section, we will discuss the difference between a parallelogram and a quadrilateral
Difference Between Parallelogram and Quadrilateral
Both quadrilateral and parallelogram are four sided geometrical figures. A parallelogram is a quadrilateral because it has four sides. All four sides figures can be called quadrilaterals. The sum of interior angles of both the figures is equal to 360 degrees. Parallelogram and quadrilateral are different because a parallelogram has four sides and the length of opposite sides is the same. The opposite sides of the parallelogram are also parallel and opposite angles are congruent. On the other hand, a quadrilateral can be any four-sided figure that may or may not have opposite sides of the same length. The opposite angles of the quadrilateral may or may not be equal or supplementary. Moreover, it is not necessary that the opposite sides of the quadrilateral are parallel to each other. It means that we can have a quadrilateral whose opposite sides are not parallel or equal, and opposite angles not congruent. From this, we can conclude that all parallelograms are quadrilaterals, but all quadrilaterals are not parallelograms.
Types of Parallelograms
Different types of parallelogram include square, rectangle, rhombus, rhomboid. Each type is explained below in detail.
Square
Square is a parallelogram because the opposite sides are parallel to each other. A square has 4 equal sides and 4 right angles. The diagonals of a square are equal, perpendicular and the bisectors of their angles. We can easily calculate the area or perimeter of a square, if we are given the length of one of its side. This is because all sides of the square have the same length.

Rectangle
The opposite sides of a rectangle are parallel to each other. A rectangle has equal opposite sides and 4 right angles. There are two pairs of opposite sides in a rectangle. The length of the opposite sides are the same. The diagonals of a rectangle are equal.

Rhombus
A rhombus has equal opposite angles and four equal sides. The diagonals of a rhombus are perpendicular and bisectors of the angles. It is important to note that every rhombus is a parallelogram but every parallelogram is not necessarily a rhombus.
Rhomboid
A rhomboid has equal sides which are parallel to the opposite sides. All angles in a rhomboid are equal to 90 degrees.

Now, you know what is parallelogram and its types, let us proceed to discuss the properties of parallelograms.
Properties of Parallelogram
The properties of a parallelogram are discussed below:
- The opposite sides of a parallelogram are parallel and congruent to each other. Congruent means that the length of the opposite sides is equal.
- The opposite angles in a parallelogram are also congruent, i.e., they are of the same measure.
- The consecutive angles in a parallelogram are supplementary, i.e., if they are added up, we will get 180 degrees.
- If any one of the four angles in a parallelogram is a right angle, then all the angles will be of 90 degrees
- The two diagonals of the parallelogram bisect each other, i.e., they cut each other in half.
- Each diagonal of a parallelogram bisects it into two equal triangles.
- The parallelogram law says that the sum of square of all sides of a parallelogram is equal to the sum of square of its diagonals.
Other Features of a Parallelogram
- The area of a parallelogram is two times the area of a triangle that was created by one of its diagonals.
- The area of the parallelogram and the magnitude of the vector cross product of two adjacent sides is also the same.
- A line segment passing through the midpoint of the parallelogram bisects its area, i.e., divide it into two equal parts
- In contrast to other convex polygons, we cannot inscribe a parallelogram in a triangle that is less than twice its area
Angles of Parallelogram
We know that the parallelograms are flat, two-dimensional figures that have four angles. The opposite interior angles are congruent. The angles on the same side of a transversal are supplementary, which means that their sum is equal to 180 degrees. The sum of the interior angles of the parallelogram is equal to 360 degrees.
Area and Perimeter of a Parallelogram
Area
Area of a parallelogram refers to the region occupied by the figure in a two-dimensional plane. The formula for calculating the area of a parallelogram is given below:
Area = Base x Height
For example, consider the following parallelogram. Calculate its area

Base of the parallelogram = 15 cm
Height of the parallelogram = 9cm
Area = Base x Height
= 15 x 9
= 135 cm
Perimeter
The perimeter of any geometrical figure refers to the total distance around the shape or total length of that shape. In the same manner, the perimeter of the parallelogram is the total distance covered by boundaries of the parallelogram. To compute this value, one should know the measures of its sides. Since, the opposite sides of the parallelogram are of the same length, hence we can use the following formula to compute the perimeter of a parallelogram:
Perimeter = 2(a + b)
For instance, consider the following parallelogram whose length of sides are given. Using these lengths, find the perimeter of the parallelogram.
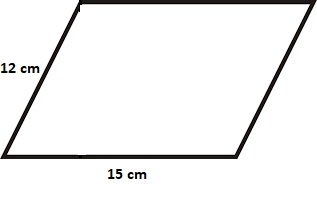
Length of one side = a = 12 cm
Length of the other side = b = 15 cm
Perimeter = 2(a + b)
= 2 (12 + 15)
= 2 (27)
= 54 cm













Hi Emma nice to meet u I love reading and solving mathematics problem