Chapters
In this article, you will learn how to calculate the area and perimeter of a triangle.
The word area refers to the region that is occupied inside the boundary of a geometrical figure or a flat object. Usually, we use square units to depict the area of an object. The standard unit of area is meters square ( . We can find areas of all the geometrical figures like circles, square, rectangles, and triangles, etc. For this purpose, we have special formulas. In the next few sections, we will discuss how to compute the areas of different types of triangles.
. We can find areas of all the geometrical figures like circles, square, rectangles, and triangles, etc. For this purpose, we have special formulas. In the next few sections, we will discuss how to compute the areas of different types of triangles.

Area of a Triangle
An area of a triangle is defined as follows:
The total region that is enclosed by three sides of a triangle is known as an area of that triangle
This area of a triangle is equal to the half of the product of base and height of a triangle. Mathematically, we can write the formula of area of a triangle like this:
Area = 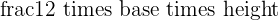
It means that to calculate the area of a triangle, we should know the base and height of the triangle. It should be kept in mind that the base and height of a triangle are perpendicular to each other. Sometimes, the height of a triangle is unknown. To find the area of such a triangle, we need to know the height first. In these situations, we different formulas to compute the areas of triangle. All these scenarios are discussed below with examples.
Area of a Triangle When Height is Known
In this section, we will see how to calculate the area of a triangle with known height.
Find the area of the following triangle:
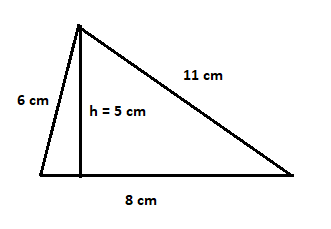
In the above triangle, height and base of the triangle is given, so we will use the general formula for finding the area of the triangle.
Area = 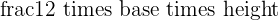
Area = 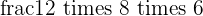
Area = 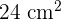
Area of an Equilateral Triangle (Height Unknown)
All sides of an equilateral triangle are equal. The formula to calculate the area of an equilateral triangle is given below:
Area = 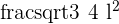
For example, consider an equilateral triangle below whose measurement of one side is given:
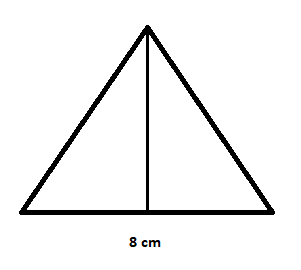
We will substitute 8 in the above formula to calculate the area of an equilateral triangle:
Area = 
Area = 
Area = 
Area of an Isosceles Triangle with Known Sides Only
Isosceles triangle is a triangle whose length of two sides are equal. We can have a situation in which the sides of an isosceles triangle are known, but the height is unknown. In this situation, we can use the following formula to compute the area of a triangle:
Area = 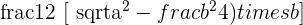
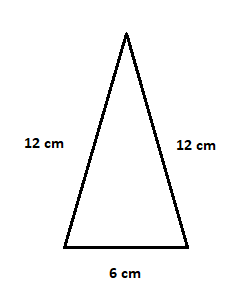
In the above triangle, the lengths of two sides are equal, hence it is an isosceles triangle. We do not know the height of the triangle, so we will use the above discussed formula to compute its area.
Area = 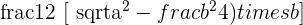
Area = 
Area = 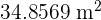
We know that remembering all the above formulas for equilateral or isosceles can be difficult. When sides are known and height is unknown, you can simply use the Heron's formula which is discussed below to calculate the area of a triangle. This is true for all types of triangles whether they are equilateral, isosceles, right angle or squalene.
Heron's Formula to Calculate the Area When Sides are Known Only
We can also use the Heron's formula to calculate the area of a triangle when the length of three sides are known. To employ this formula, we should know the perimeter of a triangle which refers to the distance covered around the triangle and is computed by summing up the length of all three sides of the triangle. Use the following steps to calculate the area using Heron's formula:
- In the first step of the process, find the semi perimeter of the triangle by summing up the three sides and dividing the figure by 2. Semi perimeter is simply half of the perimeter of a triangle.
- In the second step, apply the value obtained in the first step of the triangle in the main formula which is known as Heron's formula.
The Heron's formula to calculate the area of a triangle is given below:
Area = 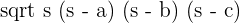
Here, s is the semi perimeter and a, b and c represent the sides of the triangle.
Consider the following example:
Find the area of the following triangle:
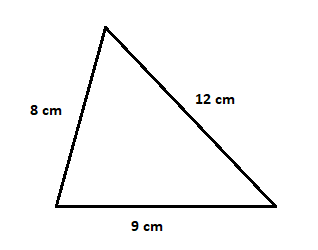
The values of sides a, b and c are 12 cm, 9 cm and 8 cm. First we will calculate the semi perimeter by substituting these values in the below formula:
Semi perimeter = 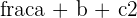
Semi perimeter = 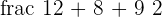
Semi perimeter = 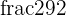
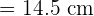
Now, we will substitute this value of semi perimeter in the below formula to find the area:
Area = 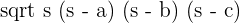
Area = 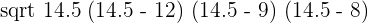
Area = 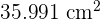
Consider another example below
Find the area of the following triangle:
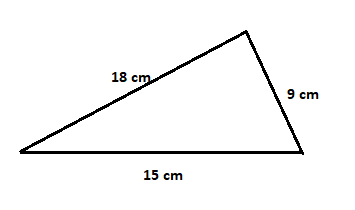
The values of sides a, b and c are 18 cm, 15 cm and 9 cm. First we will calculate the semi perimeter by substituting these values in the below formula:
Semi perimeter = 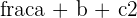
Semi perimeter = 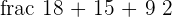
Semi perimeter = 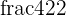

Now, we will substitute this value of semi perimeter in the below formula to find the area:
Area = 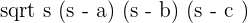
Area = 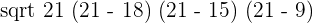
Area = 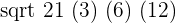
Area = 
Perimeter of a Triangle
The perimeter of any two-dimensional figure refers to a distance around the figure. We can compute the perimeter of any closed figure by just summing up the length of all the three sides. In this section, you will learn how to calculate the perimeter of different types of triangles when there lengths are known.
Formula
The formula for finding the perimeter of a triangle is given below:
Perimeter = Sum of three sides
The standard unit of perimeter is meter or centimeter.
The following table shows the formula for computing the sides of three types of triangle:
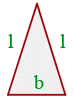
| Equilateral Triangle | Isosceles Triangle | Scalene Triangle |
 | 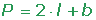 | 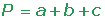 |
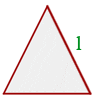 |  |  |
- It shows that the perimeter of an equilateral triangle is 3 times its length
- The perimeter of an isosceles triangle is the sum of 2 times length of the equal sides and base
- The perimeter of the scalene triangle is equal to the sum of the lengths of all three sides of the triangle
Consider the following triangle whose lengths of three sides are given:

The length of the sides are 12cm 9 cm and 8 cm respectively. To calculate the perimeter, substitute these values in the formula below:
Perimeter = a + b + c
= 12 + 9 + 8 = 29 cm













Hi Emma nice to meet u I love reading and solving mathematics problem