Chapters
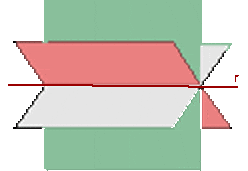
In mathematics, a sheaf of planes refers to the set of all planes that contain the same common line. It is also referred to as a pencil or fan of planes. To comprehend the sheaf of planes, consider the concept of the line at infinity where a set of parallel planes can be viewed as a sheaf of planes intersecting in a line at infinity. In other words, we can say that a sheaf of plane is the set of all planes through a line. This line is also known as the axis of the sheaf, and the sheaf itself is sometimes referred to as a pencil.
The following figure shows a sheaf of planes with an axis, r. You can see here that a set of planes contain the common line r.

Finding the Equation of the Sheaf of Planes
If the line is:
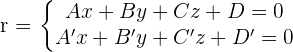
The equation of the sheaf of planes with axis, r, is:
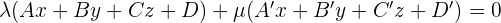
Dividing by λ and making 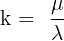 , the equation becomes:
, the equation becomes:
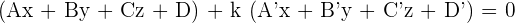
In the next section, we will be solving a couple of examples in which we will find the equation of the plane that passes through certain points and belongs to the sheaf of planes with an axis on the line.
Example 1
Find the equation of plane that passes through the point (1, 2, 4) and belongs to the sheaf of planes with its axis on the following line:
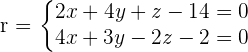
Solution
As we know that the equation of the sheaf of planes with axis, r, is:
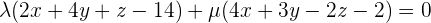
When we divide it by λ and substitute 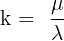 , the equation becomes:
, the equation becomes:
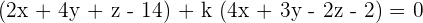
Plug values if x, y, and z in the above equation to find the value of k:
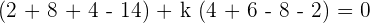
This shows that k = 1
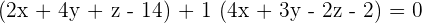
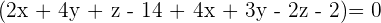
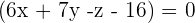
So, the equation of the plane passing through the points 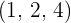 is
is 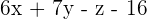 .
.
Example 2
Find the equation of plane that passes through the point (2, -1, 3) and belongs to the sheaf of planes with its axis on the following line:
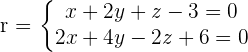
Solution
As we know that the equation of the sheaf of planes with axis, r, is:
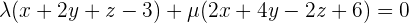
When we divide it by λ and substitute 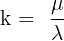 , the equation becomes:
, the equation becomes:
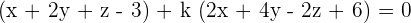
Plug values if x, y, and z in the above equation to find the value of k:
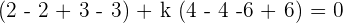
This shows that k = 1
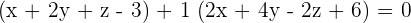
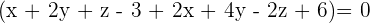
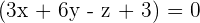
So, the equation of the plane passing through the points 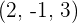 is
is 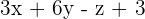 .
.
Example 3
Find the equation of plane that passes through the point (1, -2, 3) and belongs to the sheaf of planes with its axis on the following line:
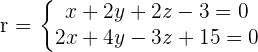
Solution
As we know that the equation of the sheaf of planes with axis, r, is:
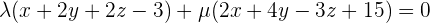
When we divide it by λ and substitute 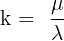 , the equation becomes:
, the equation becomes:
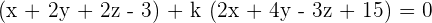
Plug values if x, y, and z in the above equation to find the value of k:

This shows that k = 1
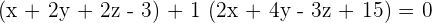

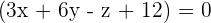
So, the equation of the plane passing through the points  is
is 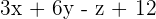 .
.
Example 4
Find the equation of plane that passes through the point (-2, 4, 1) and belongs to the sheaf of planes with its axis on the following line:

Solution
As we know that the equation of the sheaf of planes with axis, r, is:
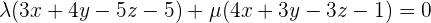
When we divide it by λ and substitute 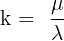 , the equation becomes:
, the equation becomes:
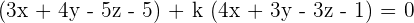
Plug values if x, y, and z in the above equation to find the value of k:
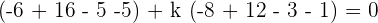
This shows that k = 1
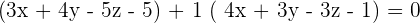
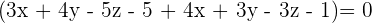
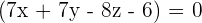
So, the equation of the plane passing through the points 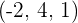 is
is 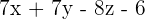 .
.
Example 5
Find the equation of plane that passes through the point (-1, -5, 2) and belongs to the sheaf of planes with its axis on the following line:

Solution
As we know that the equation of the sheaf of planes with axis, r, is:
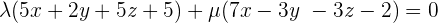
When we divide it by λ and substitute 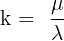 , the equation becomes:
, the equation becomes:
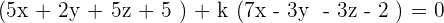
Plug values if x, y, and z in the above equation to find the value of k:

This shows that k = 1
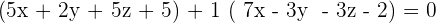
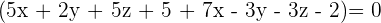
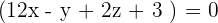
So, the equation of the plane passing through the points 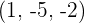 is
is 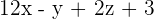 .
.
Example 6
Find the equation of plane that passes through the point (2, 4, 6) and belongs to the sheaf of planes with its axis on the following line:
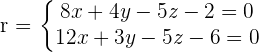
Solution
As we know that the equation of the sheaf of planes with axis, r, is:

When we divide it by λ and substitute 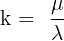 , the equation becomes:
, the equation becomes:

Plug values if x, y, and z in the above equation to find the value of k:
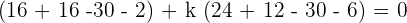
This shows that k = 1
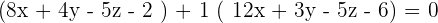
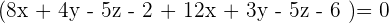
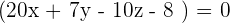
So, the equation of the plane passing through the points  is
is 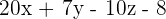 .
.
Parallel Sheaf of Planes

Two planes are parallel if the coefficients x, y, z are proportional to their equations but their independent terms are not.
All planes that are parallel to a given plane admit an equation in the form:
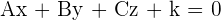 , where
, where 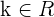
Example
Find the equation of the plane that passes through the point (3, −1, 2) and is parallel to  .
.
Solution
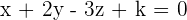
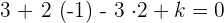
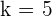
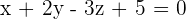













Hi Emma nice to meet u I love reading and solving mathematics problem